【题目】某校八年级有800名学生,在一次跳绳模拟测试中,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:

(1)本次抽取到的学生人数为______,扇形统计图中![]() 的值为______.
的值为______.
(2)本次调查获取的样本数据的众数是_____(分),中位数是_____(分).
(3)根据样本数据,估计我校八年级模拟体测中得12分的学生约有多少人?
参考答案:
【答案】(1)50;28;(2)12,11;(3)八年级模拟体测中得12分的学生约有256人.
【解析】
(1)根据得8分的学生人数和所占的百分比可以求得本次调查的人数,然后根据扇形统计图中的数据可以求得m的值;
(2)根据统计图中的数据可以求得本次调查获取的样本数据的众数和中位数;
(3)根据统计图中的数据可以计算出我校九年级模拟模拟体测中得12分的学生约有多少人.
:(1)本次抽取到的学生人数为:4÷8%=50,m%=1-8%-10%-22%-32%=28%,
故答案为:50,28;
(2)本次调查获取的样本数据的众数是12分,中位数是11分;
(3)800×32%=256人;
答:八年级模拟体测中得12分的学生约有256人;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的面积为24,点D在线段AC上,点D在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品现在售价为每件60元,每星期可卖出300件,市场调查反映:调整价格,每件涨价1元,每星期要少卖出10件;每件降价1元,每星期可多卖出20件.已知商品的进价为每件40元.
(1)设每件降价x元,每星期的销售利润为y元;
① 请写出y与x之间的函数关系式;
② 确定x的值,使利润最大,并求出最大利润;
(2)若涨价x元,则x= 元时,利润y的最大值为 元(直接写出答案,不必写过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,
 ,
,  ,△CDE中,
,△CDE中,  ,CD=DE=5,
,CD=DE=5,连接接BE,取BE中点F,连接AF、DF.
(1)如图1,若
 三点共线,
三点共线,  为
为 中点.
中点.①直接指出
 与
与 的关系______________;
的关系______________;②直接指出
 的长度______________;
的长度______________;(2)将图(1)中的△CDE绕
 点逆时针旋转
点逆时针旋转 (如图2,
(如图2,  ),试确定
),试确定 与
与 的关系,并说明理由;
的关系,并说明理由;(3)在(2)中,若
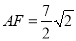 ,请直接指出点
,请直接指出点 所经历的路径长.
所经历的路径长.

图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 交
交 轴于点
轴于点 、点
、点 ,交
,交 轴于点C,且S△ABC=6.
轴于点C,且S△ABC=6.(1)求
 两点的坐标;
两点的坐标;(2)求△ABC的外接圆与抛物线的对称轴的交点坐标;
(3)点E为抛物线上的一动点(点
 异于
异于 ,且
,且 在对称轴右侧),直线
在对称轴右侧),直线 交对称轴于N,
交对称轴于N,直线BE交对称轴于
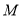 ,对称轴交
,对称轴交 轴于
轴于 ,试确定
,试确定 、
、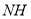 的数量关系并说明理由.
的数量关系并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,A(-1,5)、B(-1,0),C(-4,3).
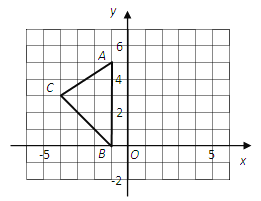
(1)△ABC的面积是 .
(2)在下图中画出△ABC向下平移2个单位,向右平移5个单位后的△A1B1C1.
(3)写出点A1、B1、C1的坐标.
-
科目: 来源: 题型:
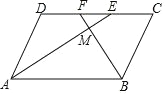
查看答案和解析>>【题目】如图,在 ABCD 中,AE、BF 分别平分∠DAB 和∠ABC,交 CD 于点 E、F,AE、BF 相交于点 M.
(1)求证:AE⊥BF;
(2)判断线段 DF 与 CE 的大小关系,并予以证明.
相关试题

