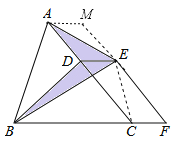
【题目】如图,已知△ABC的面积为24,点D在线段AC上,点D在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积是_____.

参考答案:
【答案】8
【解析】
连接EC,过A作AM∥BC交FE的延长线于M,求出平行四边形ACFM,根据等底等高的三角形面积相等得出△BDE的面积和△CDE的面积相等,△ADE的面积和△AME的面积相等,推出阴影部分的面积等于平行四边形ACFM的面积的一半,求出CF×hCF的值即可.
连接DE、EC,过A作AM∥BC交FE的延长线于M,
∵四边形CDEF是平行四边形,
∴DE∥CF,EF∥CD,
∴AM∥DE∥CF,AC∥FM,
∴四边形ACFM是平行四边形,
∵△BDE边DE上的高和△CDE的边DE上的高相同,
∴△BDE的面积和△CDE的面积相等,
同理△ADE的面积和△AME的面积相等,
即阴影部分的面积等于平行四边形ACFM的面积的一半,是![]() ×CF×hCF,
×CF×hCF,
∵△ABC的面积是24,BC=3CF
∴![]() BC×hBC=
BC×hBC=![]() ×3CF×hCF=24,
×3CF×hCF=24,
∴CF×hCF=16,
∴阴影部分的面积是![]() ×16=8,
×16=8,
故答案为:8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三张形状、大小相同但画面不同的风景图片,都按同样的方式剪成相同的三段,然后将上、中、下三段分别混合洗匀,从三堆图片中随机各抽出一张, 求这三张图片恰好组成一张完整风景图片的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某小区规划在一个长34m、宽22m的矩形ABCD上,修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为100m2,那么通道的宽应设计成____m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠ =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品现在售价为每件60元,每星期可卖出300件,市场调查反映:调整价格,每件涨价1元,每星期要少卖出10件;每件降价1元,每星期可多卖出20件.已知商品的进价为每件40元.
(1)设每件降价x元,每星期的销售利润为y元;
① 请写出y与x之间的函数关系式;
② 确定x的值,使利润最大,并求出最大利润;
(2)若涨价x元,则x= 元时,利润y的最大值为 元(直接写出答案,不必写过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,
 ,
,  ,△CDE中,
,△CDE中,  ,CD=DE=5,
,CD=DE=5,连接接BE,取BE中点F,连接AF、DF.
(1)如图1,若
 三点共线,
三点共线,  为
为 中点.
中点.①直接指出
 与
与 的关系______________;
的关系______________;②直接指出
 的长度______________;
的长度______________;(2)将图(1)中的△CDE绕
 点逆时针旋转
点逆时针旋转 (如图2,
(如图2,  ),试确定
),试确定 与
与 的关系,并说明理由;
的关系,并说明理由;(3)在(2)中,若
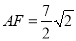 ,请直接指出点
,请直接指出点 所经历的路径长.
所经历的路径长.

图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级有800名学生,在一次跳绳模拟测试中,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:

(1)本次抽取到的学生人数为______,扇形统计图中
 的值为______.
的值为______.(2)本次调查获取的样本数据的众数是_____(分),中位数是_____(分).
(3)根据样本数据,估计我校八年级模拟体测中得12分的学生约有多少人?
相关试题

