【题目】已知△ABC中, ![]() ,
, ![]() ,△CDE中,
,△CDE中, ![]() ,CD=DE=5,
,CD=DE=5,
连接接BE,取BE中点F,连接AF、DF.
(1)如图1,若![]() 三点共线,
三点共线, ![]() 为
为![]() 中点.
中点.
①直接指出![]() 与
与![]() 的关系______________;
的关系______________;
②直接指出![]() 的长度______________;
的长度______________;
(2)将图(1)中的△CDE绕![]() 点逆时针旋转
点逆时针旋转![]() (如图2,
(如图2, ![]() ),试确定
),试确定![]() 与
与![]() 的关系,并说明理由;
的关系,并说明理由;
(3)在(2)中,若![]() ,请直接指出点
,请直接指出点![]() 所经历的路径长.
所经历的路径长.


图1 图2
参考答案:
【答案】(1)①![]() ,
, ![]() ,②
,②![]() ;(2)
;(2)![]() ,
, ![]() ,理由见解析;(3)
,理由见解析;(3)![]() 或
或![]()
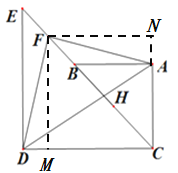
【解析】试题分析:(1)①如图,过点F M⊥CD于M,FN⊥AC交CA的延长线于点N,根据已知条件易证四边形FMCN为正方形,可得FN=FM,再证△FNA≌△FMD,即可得∠NFA=∠DFM,DF=AF,所以∠NFA+∠AFM=∠DFM+∠AFM=∠DFA=90°,即可证得![]() ;②根据勾股定理求得BC=
;②根据勾股定理求得BC=![]() ,EC=5
,EC=5![]() ,因
,因![]() 为
为![]() 中点,F为BE的中点,可得CH=BH=
中点,F为BE的中点,可得CH=BH=![]() ,EB=5
,EB=5![]() -
-![]() =
=![]() ,EF=BF=
,EF=BF=![]() ,所以FH=BF+BH=
,所以FH=BF+BH=![]() ;
;
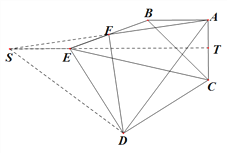
(2) ![]() ,
, ![]() ,延长
,延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,
, ![]() ,
, ![]() ,
, ![]() ,再证得
,再证得![]() ,由
,由![]() ,CD=DE,根据SAS判定
,CD=DE,根据SAS判定![]() ,
, ![]() ,
, ![]() ,
, ![]() ,根据等腰直角三角形的性质可得
,根据等腰直角三角形的性质可得![]() ,
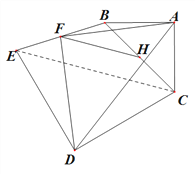
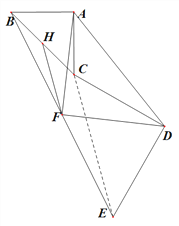
, ![]() ; (3)如图,当旋转
; (3)如图,当旋转![]() 或
或![]() 时,
时, ![]() ,AD=7,点
,AD=7,点![]() 经历的路径长为
经历的路径长为![]() 或
或![]() .
.
试题解析:
(1)(1)①![]() ,
, ![]()
②![]()
(2)结论: ![]() ,
, ![]() 理由如下:
理由如下:
延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 于
于![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
(3)旋转![]() 或
或![]() 时,
时, ![]() ,AD=7,点
,AD=7,点![]() 经历的路径长为
经历的路径长为![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠ =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的面积为24,点D在线段AC上,点D在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品现在售价为每件60元,每星期可卖出300件,市场调查反映:调整价格,每件涨价1元,每星期要少卖出10件;每件降价1元,每星期可多卖出20件.已知商品的进价为每件40元.
(1)设每件降价x元,每星期的销售利润为y元;
① 请写出y与x之间的函数关系式;
② 确定x的值,使利润最大,并求出最大利润;
(2)若涨价x元,则x= 元时,利润y的最大值为 元(直接写出答案,不必写过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级有800名学生,在一次跳绳模拟测试中,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:

(1)本次抽取到的学生人数为______,扇形统计图中
 的值为______.
的值为______.(2)本次调查获取的样本数据的众数是_____(分),中位数是_____(分).
(3)根据样本数据,估计我校八年级模拟体测中得12分的学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 交
交 轴于点
轴于点 、点
、点 ,交
,交 轴于点C,且S△ABC=6.
轴于点C,且S△ABC=6.(1)求
 两点的坐标;
两点的坐标;(2)求△ABC的外接圆与抛物线的对称轴的交点坐标;
(3)点E为抛物线上的一动点(点
 异于
异于 ,且
,且 在对称轴右侧),直线
在对称轴右侧),直线 交对称轴于N,
交对称轴于N,直线BE交对称轴于
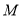 ,对称轴交
,对称轴交 轴于
轴于 ,试确定
,试确定 、
、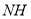 的数量关系并说明理由.
的数量关系并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,A(-1,5)、B(-1,0),C(-4,3).
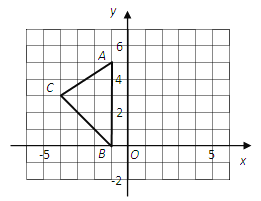
(1)△ABC的面积是 .
(2)在下图中画出△ABC向下平移2个单位,向右平移5个单位后的△A1B1C1.
(3)写出点A1、B1、C1的坐标.
相关试题

