【题目】已知:b是最小的正整数且a、b满足![]() ,试回答问题.
,试回答问题.
(1)请直接写出a、b、c的值.
a= b= c= .
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到2之间运动时(即0≤x≤2时),请化简式子:![]() (请写出化简过程)
(请写出化简过程)
![]()
(3)在(1)(2)的条件下,若点D从A点开始以每秒1的速度向左运动,同时点E从B点开始以每秒2个单位长度向右运动,点F从C点开始以每秒5个单位长度的速度向右运动,设它们运动的t秒,请问,EF﹣DE的值是否随着时间t的变化而变化?若变化,请说明理由;若不变,请求其值.
参考答案:
【答案】(1)a=-1,b=1,c=5;(2)化简为![]() ;(3)不变,EF﹣DE的值为2
;(3)不变,EF﹣DE的值为2
【解析】
(1)根据b是最小的正整数,即可确定b的值,然后根据非负数的性质,几个非负数(式)的和是0,则每个数(式)是0,即可求得a,b,c的值;
(2)根据x的范围,分别确定x+1,x-1,x-5的符号,然后根据绝对值的意义即可化简;
(3)根据D,E,F的运动情况即可确定DE,EF的变化情况,即可确定EF-DE的值.
解:(1)∵b是最小的正整数,
∴b=1.
∵![]()
∴c-5=0且a+b=0,
∴a=-1,b=1,c=5.
(2)根据题意可得
0≤x≤2,且x-1=0时,x=1
①当0≤x≤1时,原式=(x+1)+(x-1)+2(5-x)=10;
②当1<x≤2时,原式=(x+1)-(x-1)+2(5-x)=-2x+12.
故化简为![]() ;
;
(3)不变.
∵点D以每秒1个单位长度的速度向左运动,点E每秒2个单位长度向右运动,
∴D,E每秒钟增加3个单位长度;
∵点E和点F分别以每秒2个单位长度和5个单位长度的速度向右运动,
∴E,F每秒钟增加3个单位长度.
∴EF-DE=2,EF-DE的值不随着时间t的变化而改变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)(+19)+(﹣27)﹣(+10)﹣23+(﹣49)
(2)(
 )×(﹣30)
)×(﹣30)(3)
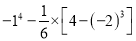
(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OM是∠AOC的平分线.ON是∠BOC的平分线.
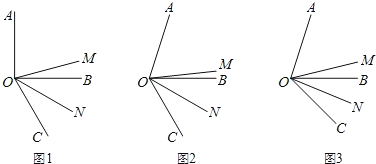
(1)如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?
(2)如图2,当∠AOB=70°,∠BOC=60°时,∠MON= (直接写出结果)
(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON﹣∠CON= (直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0),则点D的坐标为( )
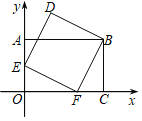
A. (1,2.5)B. (1,1+
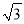 )C. (1,3)D. (
)C. (1,3)D. (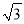 ﹣1,1+
﹣1,1+ 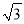 )
) -
科目: 来源: 题型:
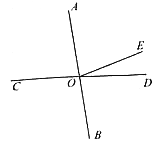
查看答案和解析>>【题目】如图,AB、CD交于点O,∠AOE=4∠DOE,∠AOE的余角比∠DOE小10°(题中所说的角均是小于平角的角).
(1)求∠AOE的度数;
(2)请写出∠AOC在图中的所有补角;
(3)从点O向直线AB的右侧引出一条射线OP,当∠COP=∠AOE+∠DOP时,求∠BOP的度数.
-
科目: 来源: 题型:
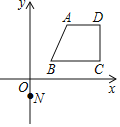
查看答案和解析>>【题目】如图,过点N(0,-1)的直线y=kx+b与图中的四边形ABCD有不少于两个交点,其中A(2,3)、B(1,1)、C(4,1)、D(4,3),则k的取值范围____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举办“校园好声音”朗诵大赛,根据初赛成绩,七年级和八年级各选出5名选手组成七年级代表队和八年级代表队参加学校决赛两个队各选出的5名选手的决赛成绩如图所示:
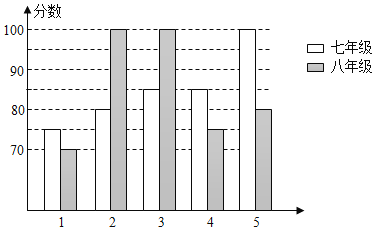
(1)根据所给信息填写表格;
平均数(分)
中位数(分)
众数(分)
七年级
85
八年级
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)若七年级代表队决赛成绩的方差为70,计算八年级代表队决赛成绩的方差,并判断哪个代表队的选手成绩较为稳定.
相关试题

