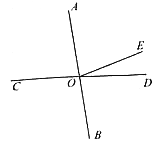
【题目】如图,AB、CD交于点O,∠AOE=4∠DOE,∠AOE的余角比∠DOE小10°(题中所说的角均是小于平角的角).
(1)求∠AOE的度数;
(2)请写出∠AOC在图中的所有补角;
(3)从点O向直线AB的右侧引出一条射线OP,当∠COP=∠AOE+∠DOP时,求∠BOP的度数.
参考答案:
【答案】(1)∠AOE=80°;(2)∠AOD、∠BOC、∠BOE;(3),∠BOP的度数为130°或30°.
【解析】
(1)根据余角的定义及题意可得∠DOE=100°-∠AOE,再由∠AOE=4∠DOE即可求得∠AOE的度数;(2)根据补角的定义可得∠AOC+∠AOD=180°,∠AOC+∠BOC=180°,根据已知条件及(1)的结论可证得∠AOC+∠BOE=180°,即可得∠AOC的补角有∠AOD、∠BOC、∠BOE;(3)根据已知条件求得∠COP=130°, ∠DOP=50°,再分OP在直线CD上方和下方两种情况求解即可.
(1)∵∠AOE的余角比∠DOE小10°,
∴90°-∠AOE=∠DOE-10°,
∴∠DOE=100°-∠AOE
∵∠AOE=4∠DOE,
∴∠AOE=4(100°-∠AOE)
∴∠AOE=80°,
即:∠AOE的度数为80°;
(2)由题意可知:∠AOC+∠AOD=180°,∠AOC+∠BOC=180°,
∴∠AOC的补角有:∠AOD、∠BOC;
∵∠AOE=4∠DOE,∠AOE=80°,
∴∠DOE=20°,
∴∠AOD=∠AOE+∠DOE=100°,
∴∠BOD=∠AOC =80°,
∴∠BOE=∠BOD+∠DOE=80°+20°=100°,
∴∠AOC+∠BOE=80°+100°=180°.
∴∠BOE是∠AOC的补角.
综上,∠AOC的补角有:∠AOD、∠BOC、∠BOE;
(3)由(1)可得∠AOE=80°,∠DOE=![]() ∠AOE =20°,
∠AOE =20°,
∴∠AOD=∠AOE+∠DOE=100°,∠BOD=180°-∠A OD=80°,
∵∠COP=∠AOE+∠DOP,
∴∠COP-∠DOP =∠AOE=80°,
∵∠COP+∠DOP=180°,
∴∠COP=130°, ∠DOP=50°,
当OP在直线CD上方时(如图),

∴∠BOP=∠BOD+ ∠DOP=80°+50°=130°;

∠BOP=∠BOD- ∠DOP=80°-50°=-30°;
综上,∠BOP的度数为130°或30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.
(1)利用图1,求证:四边形ABCD是菱形.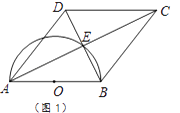
(2)如图2,若CD的延长线与半圆相切于点F,已知直径AB=8. ①连结OE,求△OBE的面积.
②求弧AE的长.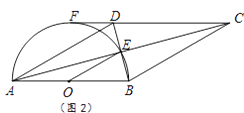
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列三行数,并完成后面的问题:
①-2,4,-8,16,……
②1,-2,4,-8,……
③0,-3,3,-9,……
(1)思考第①行数的规律,写出第
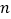 个数字是________;
个数字是________;(2)设第②行第
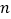 个数为
个数为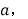 第③行第
第③行第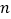 个数为
个数为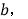 请直接写出
请直接写出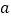 与
与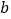 之间的关系;
之间的关系;(3)设
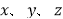 分别表示第①、②、③行数的第2019个数字,求
分别表示第①、②、③行数的第2019个数字,求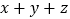 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为________________________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下表中有两种移动电话计费方式:
月使用费
主叫限定时间(分钟)
主叫超时费(元/分钟)
被叫
方式一
65
160
0.20
免费
方式二
100
380
0.25
免费
(月使用费固定收;主叫不超过限定的时间不再收费,主叫超过限定时间的部分加收超时费;被叫免费)
(1)若张聪某月主叫通话时间为200分钟,则他按方式一计费需____元,按方式二计费需____
元;李华某月按方式二计费需107元,则李华该月主叫通话时间为_____分钟;
(2)是否存在某主叫通话时间
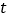 (分钟),按方式一和方式二的计费相等?若存在,请求出
(分钟),按方式一和方式二的计费相等?若存在,请求出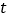 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。(3)直接写出当月主叫通话时间
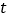 (分钟)满足什么条件时,选择方式一省钱。
(分钟)满足什么条件时,选择方式一省钱。 -
科目: 来源: 题型:
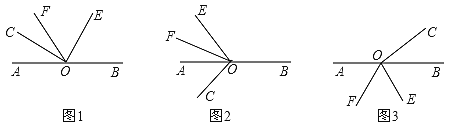
查看答案和解析>>【题目】已知O为直线AB上的一点,∠COE是直角,OF平分∠AOE(图中所说的角都是小于平角的角).
(1)如图1,若∠COF=28°,则∠BOE=______°;若∠COF=
 则∠BOE=_______;∠BOE与∠COF的数量关系为_________;
则∠BOE=_______;∠BOE与∠COF的数量关系为_________;(2)将∠COE绕点O逆时针旋转到如图2所示的位置时,(1)中∠BOE和∠COF的数量关系否仍然成立?若成立,请说明理由?若不成立,求出∠BOE与∠COF的数量关系;
(3)当∠COE绕点O顺时针旋转到如图3的位置时,(1)中∠BOE和∠COF的数量关系是否仍然成立?若成立,请说明理由;若不成立,请求出∠BOE与∠COF的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A,B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=
 x+4,与x轴相交于点D.
x+4,与x轴相交于点D.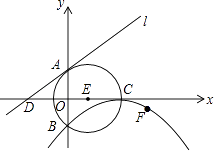
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3)动点P在抛物线上,当点P到直线l的距离最小时,求出点P的坐标及最小距离.
相关试题

