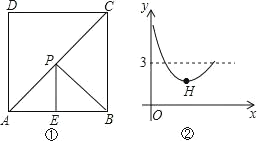
【题目】如图①,在正方形ABCD中,点E是AB的中点,点P是对角线AC上一动点。设PC的长度为x,PE与PB的长度和为y,图②是y关于x的函数图象,则图象上最低点H的坐标为( )
A. (1,2)B. (![]() )C.
)C. 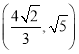 D.
D. ![]()
参考答案:
【答案】C
【解析】
如图,连接PD.由B、D关于AC对称,推出PB=PD,推出PB+PE=PD+PE,推出当D、P、E共线时,PE+PB的值最小,观察图象可知,当点P与A重合时,PE+PB=3,推出AE=EB=1,AD=AB=2,分别求出PB+PE的最小值,PC的长即可解决问题.
如图,连接PD.
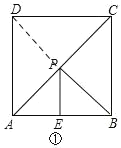
∵B、D关于AC对称,
∴PB=PD,
∴PB+PE=PD+PE,
∴当D、P、E共线时,PE+PB的值最小,如下图:
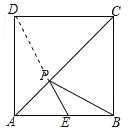
当点P与A重合时,PE+PB=3,
![]() ,AD=AB=2
,AD=AB=2
在RT△AED中,DE=![]()
![]() 点H的纵坐标为
点H的纵坐标为![]()
![]()
![]()
![]()
![]()
![]()
![]() 点H的横坐标为
点H的横坐标为![]()
![]() H
H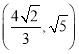
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,ED⊥BD,连接AC,EC.已知AB=5,DE=2,BD=12,设CD=x.
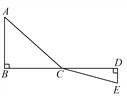
(1)用含x的代数式表示AC+CE的长;
(2)请问点C在BD上什么位置时,AC+CE的值最小?
(3)根据(2)中的规律和结论,请构图求出代数式
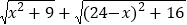 的最小值.
的最小值. -
科目: 来源: 题型:
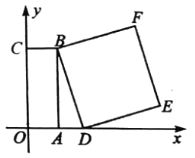
查看答案和解析>>【题目】如图,以矩形
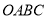 的顶点
的顶点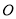 为坐标原点,
为坐标原点,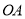 所在直线为
所在直线为 轴,
轴,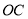 所在直线为
所在直线为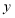 轴,建立平面直角坐标系.已知,
轴,建立平面直角坐标系.已知,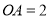 ,
,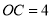 ,点
,点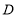 为
为 轴上一动点,以
轴上一动点,以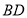 为一边在
为一边在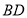 右侧作正方形
右侧作正方形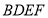 .
.
(1)若点
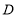 与点
与点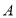 重合,请直接写出点
重合,请直接写出点 的坐标.
的坐标.(2)若点
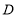 在
在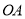 的延长线上,且
的延长线上,且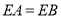 ,求点
,求点 的坐标.
的坐标.(3)若
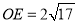 ,求点
,求点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,二次函数
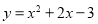 的图象如图所示,点
的图象如图所示,点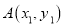 ,
,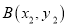 是该二次函数图象上的两点,其中
是该二次函数图象上的两点,其中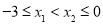 ,则下列结论正确的是( )
,则下列结论正确的是( )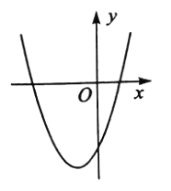
A.
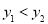 B.
B. 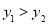 C. 函数
C. 函数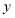 的最小值是
的最小值是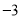 D. 函数
D. 函数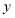 的最小值是
的最小值是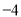
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为非零的实数,则
 的可能值的个数为( )
的可能值的个数为( )A. 4 B. 5 C. 6 D. 7
-
科目: 来源: 题型:
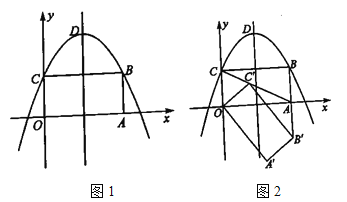
查看答案和解析>>【题目】如图1,以矩形
 的顶点
的顶点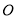 为原点,
为原点,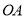 所在直线为
所在直线为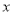 轴,
轴,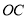 所在直线为
所在直线为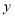 轴,建立平面直角坐标系,顶点为点
轴,建立平面直角坐标系,顶点为点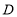 的抛物线
的抛物线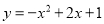 经过点
经过点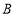 ,点
,点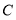 .
.
(1)写出抛物线的对称轴及点
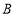 的坐标,
的坐标,(2)将矩形
 绕点
绕点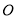 顺时针旋转
顺时针旋转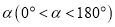 得到矩形
得到矩形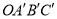 .
.①当点
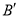 恰好落在
恰好落在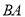 的延长线上时,如图2,求点
的延长线上时,如图2,求点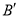 的坐标.
的坐标.②在旋转过程中,直线
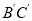 与直线
与直线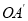 分别与抛物线的对称轴相交于点
分别与抛物线的对称轴相交于点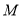 ,点
,点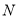 .若
.若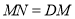 ,求点
,求点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
相关试题

