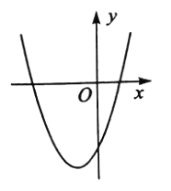
【题目】在平面直角坐标系中,二次函数![]() 的图象如图所示,点
的图象如图所示,点![]() ,
,![]() 是该二次函数图象上的两点,其中
是该二次函数图象上的两点,其中![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A. ![]() B.
B. ![]() C. 函数
C. 函数![]() 的最小值是
的最小值是![]() D. 函数
D. 函数![]() 的最小值是
的最小值是![]()
参考答案:
【答案】D
【解析】
根据抛物线解析式求得抛物线的顶点坐标,结合函数图象的增减性进行解答.
![]() =(x+3)(x1),
=(x+3)(x1),
则该抛物线与x轴的两交点横坐标分别是3、1.
又![]() =
=![]() ,
,
∴该抛物线的顶点坐标是(1,4),对称轴为x=-1.
A. 无法确定点A. B离对称轴x=1的远近,故无法判断y![]() 与y
与y![]() 的大小,故本选项错误;
的大小,故本选项错误;
B. 无法确定点A. B离对称轴x=1的远近,故无法判断y![]() 与y
与y![]() 的大小,故本选项错误;
的大小,故本选项错误;
C. y的最小值是4,故本选项错误;
D. y的最小值是4,故本选项正确。
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,ED⊥BD,连接AC,EC.已知AB=5,DE=2,BD=12,设CD=x.
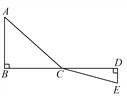
(1)用含x的代数式表示AC+CE的长;
(2)请问点C在BD上什么位置时,AC+CE的值最小?
(3)根据(2)中的规律和结论,请构图求出代数式
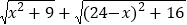 的最小值.
的最小值. -
科目: 来源: 题型:
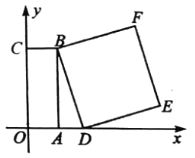
查看答案和解析>>【题目】如图,以矩形
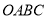 的顶点
的顶点 为坐标原点,
为坐标原点,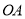 所在直线为
所在直线为 轴,
轴,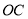 所在直线为
所在直线为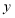 轴,建立平面直角坐标系.已知,
轴,建立平面直角坐标系.已知,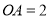 ,
,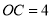 ,点
,点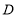 为
为 轴上一动点,以
轴上一动点,以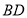 为一边在
为一边在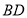 右侧作正方形
右侧作正方形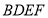 .
.
(1)若点
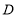 与点
与点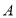 重合,请直接写出点
重合,请直接写出点 的坐标.
的坐标.(2)若点
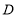 在
在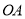 的延长线上,且
的延长线上,且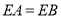 ,求点
,求点 的坐标.
的坐标.(3)若
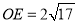 ,求点
,求点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在正方形ABCD中,点E是AB的中点,点P是对角线AC上一动点。设PC的长度为x,PE与PB的长度和为y,图②是y关于x的函数图象,则图象上最低点H的坐标为( )
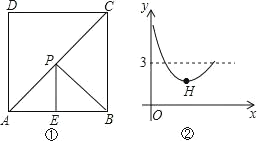
A. (1,2)B. (
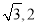 )C.
)C. 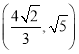 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为非零的实数,则
 的可能值的个数为( )
的可能值的个数为( )A. 4 B. 5 C. 6 D. 7
-
科目: 来源: 题型:
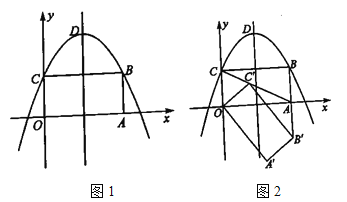
查看答案和解析>>【题目】如图1,以矩形
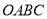 的顶点
的顶点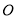 为原点,
为原点,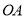 所在直线为
所在直线为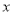 轴,
轴,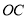 所在直线为
所在直线为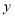 轴,建立平面直角坐标系,顶点为点
轴,建立平面直角坐标系,顶点为点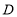 的抛物线
的抛物线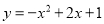 经过点
经过点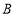 ,点
,点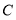 .
.
(1)写出抛物线的对称轴及点
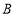 的坐标,
的坐标,(2)将矩形
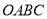 绕点
绕点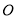 顺时针旋转
顺时针旋转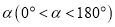 得到矩形
得到矩形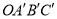 .
.①当点
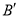 恰好落在
恰好落在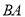 的延长线上时,如图2,求点
的延长线上时,如图2,求点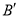 的坐标.
的坐标.②在旋转过程中,直线
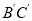 与直线
与直线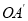 分别与抛物线的对称轴相交于点
分别与抛物线的对称轴相交于点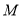 ,点
,点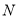 .若
.若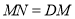 ,求点
,求点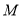 的坐标.
的坐标.
相关试题

