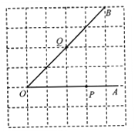
【题目】如图,点P,Q分别是∠AOB的边OA,OB上的点.
(1)过点P画OB的垂线,垂足为H;
(2)过点Q画OA的垂线,交OA于点C,连接PQ;
(3)线段QC的长度是点Q到 的距离, 的长度是点P到直线OB的距离,因为直线外一点和直线上各点连接的所有线段中,垂线段最短,所以线段PQ、PH的大小关系是 (用“<”号连接).
参考答案:
【答案】(1)画图见解析;(2)见解析;(3)直线OA,线段PH;PH<PQ.
【解析】
(1)根据垂线的概念、结合网格特点作图即可;(2)根据垂线的概念、结合网格特点和线段的作法作图;(3)根据垂线段最短进行比较即可.
(1)如图,直线PH即为所求;
(2)如图,直线QC即为所求;
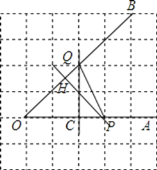
(3)线段QC的长度是点Q到直线OA的距离,线段PH的长度是点P到直线OB的距离,
根据直线外一点和直线上各点连接的所有线段中,垂线段最短可知PH<PQ,
故答案为:直线OA,线段PH;PH<PQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为 ;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市在一次市政施工中,有两段长度相等的人行道铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设人行道的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
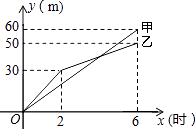
(1)求乙队在2≤x≤6的时间段内,y与x的函数关系式;
(2)若甲队施工速度不变,乙队在施工6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完成,所铺设的人行道共是多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,茬四边形ABCD中,AD∥BC,E是BC的中点,AC平分∠BCD,且AC⊥AB,接DE,交AC于F.

(1)求证:AD=CE;
(2)若∠B=60°,试确定四边形ABED是什么特殊四边形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营某种品牌的玩具,购进的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具,
(1)设该种品牌玩具的销售单价为x元,请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元;
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元?
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于45元,且商场要完成不少于480件的销售任务,求商场销售该品牌玩具获得的最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0<a<21)个单位到△DEF的位置.
(1)求BC边上的高;
(2)若AB=10,
①求线段DF的长;
②连结AE,当△ABE时等腰三角形时,求a的值.

相关试题

