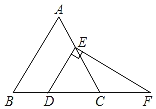
【题目】如图,△ABC是边长为5的等边三角形,点D,E分别在BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的的延长线于点F,若BD=2,则DF等于( )
A.7B.6C.5D.4
参考答案:
【答案】B
【解析】
首先根据△ABC是等边三角形,得出∠B=60°,再由DE∥AB,得出∠EDC=∠B=60°,然后由EF⊥DE,得出∠F=30°,进而得出△DEC是等边三角形,得出ED=DC=BC﹣BD,最后由∠DEF=90°,∠F=30°,得出DF=2DE=6.
∵△ABC是等边三角形,
∴∠B=60°,
∵DE∥AB,
∴∠EDC=∠B=60°,
∵EF⊥DE,
∴∠DEF=90°,
∴∠F=30°,
∵∠ACB=∠EDC=60°,
∴△DEC是等边三角形,
∴ED=DC=BC﹣BD=5﹣2=3,
∵∠DEF=90°,∠F=30°,
∴DF=2DE=6.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB的垂直平分线分别交AB,BC于D,E,AC的垂直平分线分别交AC,BC于F,G.
(1)若△AEG的周长为10,求线段BC的长.
(2)若∠BAC=128°,求∠EAG的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某活动小组为了估计装有
 个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共
个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共 组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做
组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做 次试验,汇总起来后,摸到红球次数为
次试验,汇总起来后,摸到红球次数为 次.
次. 估计从袋中任意摸出一个球,恰好是红球的概率是多少?
估计从袋中任意摸出一个球,恰好是红球的概率是多少? 请你估计袋中红球接近多少个?
请你估计袋中红球接近多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场有
 、
、 两种商品,
两种商品, 商品每件售价
商品每件售价 元,
元, 商品每件售价
商品每件售价 元,
元, 商品每件的成本是
商品每件的成本是 元.
元.根据市场调查“若按上述售价销售,该商场每天可以销售
 商品
商品 件,若销售单价毎上涨
件,若销售单价毎上涨 元,
元, 商品每天的销售量就减少
商品每天的销售量就减少 件.
件. 请写出
请写出 商品每天的销售利润
商品每天的销售利润 (元)与销售单价
(元)与销售单价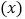 元之间的函数关系?
元之间的函数关系? 当销售单价为多少元时,
当销售单价为多少元时, 商品每天的销售利润最大,最大利润是多少?
商品每天的销售利润最大,最大利润是多少? -
科目: 来源: 题型:
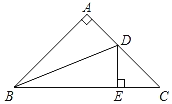
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=90°,BD是∠ABC的平分线,DE⊥BC于E,若BC=12,则△DEC的周长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解下列方程时,配方正确的是( )
A. 方程x2-6x-5=0,可化为(x-3)2=4
B. 方程y2-2y-2 015=0,可化为(y-1)2=2 015
C. 方程a2+8a+9=0,可化为(a+4)2=25
D. 方程2x2-6x-7=0,可化为

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a,b,c分别为△ABC三边的长.
(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
相关试题

