【题目】如图,在等腰直角三角形ABC中,![]() ,
,![]() ,D是AB的中点,E、F分别是AC、BC上的点(点E不与端点A、C重合),连接EF并取EF的中点O,连接DO并延长至点G,使
,D是AB的中点,E、F分别是AC、BC上的点(点E不与端点A、C重合),连接EF并取EF的中点O,连接DO并延长至点G,使![]() ,连接DE、GE、GF.
,连接DE、GE、GF.
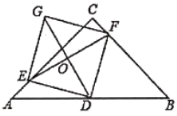
(1)求证:四边形EDFG是平行四边形;
(2)若![]() ,探究四边形EDFG的形状?
,探究四边形EDFG的形状?
(3)在(2)的条件下,当E点在何处时,四边形EDFG的面积最小,并求出最小值.
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)当E点在AC中点时,四边形EDGF的面积最小为4.
【解析】
(1)根据对角线互相平分的四边形是平行四边形可得结论;
(2)连接CD,根据等腰直角三角形的性质可得出∠A=∠DCF=45°、AD=CD,结合AE=CF可证出△ADE≌△CDF(SAS),根据全等三角形的性质可得出DE=DF、ADE=∠CDF,通过角的计算可得出∠EDF=90°,再根据(1)中的结论,由此即可证出四边形EDFG是正方形;
(3)过点D作DE′⊥AC于E′,根据等腰直角三角形的性质可得出DE′的长度,从而得出2≤DE<2![]() ,再根据正方形的面积公式即可得出四边形EDFG的面积的最小值.
,再根据正方形的面积公式即可得出四边形EDFG的面积的最小值.
(1)证明:∵O是EF的中点,
∴OE=OF,
∵OG=OD,
∴四边形EDFG是平行四边形;
(2)解:四边形EDFG是正方形,理由是:
连接CD,如图1所示,
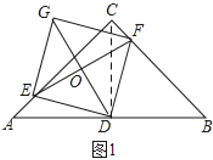
∵△ABC为等腰直角三角形,∠ACB=90°,D是AB的中点,
∴∠A=∠DCF=45°,AD=CD.
在△ADE和△CDF中,
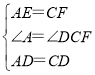 ,
,
∴△ADE≌△CDF(SAS),
∴DE=DF,∠ADE=∠CDF.
∵∠ADE+∠EDC=90°,
∴∠EDC+∠CDF=∠EDF=90°,
由(1)知:四边形EDFG是平行四边形;
∴四边形EDFG是正方形;
(3)解:过点D作DE′⊥AC于E′,如图2所示.
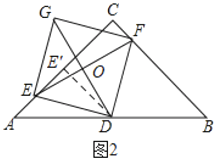
∵△ABC为等腰直角三角形,∠ACB=90°,AC=BC=4,
∴DE′=![]() BC=2,AB=4
BC=2,AB=4![]() ,点E′为AC的中点,
,点E′为AC的中点,
∴2≤DE<2![]() (点E与点E′重合时取等号).
(点E与点E′重合时取等号).
∴4≤S四边形EDFG=DE2<8.
∴当点E为线段AC的中点时,四边形EDFG的面积最小,该最小值为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段
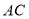 和
和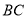 在同一直线上,如果
在同一直线上,如果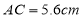 ,
,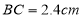 ,则线段
,则线段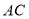 和
和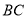 的中点之间的距离为______________
的中点之间的距离为______________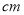 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司购买了一批A、B两种型号的产品,其中A型产品的单价比B型产品的单价多6元,已知该公司用1400元购买A型产品的件数与用1160元购买B型产品的件数相等.
(1)求该公司购买的A、B两种型号产品的单价各是多少元?
(2)若两种型号的产品共购买了100件,且购买的总费用为3260元,求购买了多少件A型产品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】简单多面体是各个面都是多边形组成的几何体,十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)和棱数(E)之间存在一个有趣的关系式,称为欧拉公式.如表是根据左边的多面体模型列出的不完整的表:
多面体
顶点数
面数
棱数
四面体
4
4
6
长方体
8
6
正八面体
8
12
现在有一个多面体,它的每一个面都是三角形,它的面数(F)和棱数(E)的和为30,则这个多面体的顶点数V=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(方法回顾)证明:三角形中位线定理.
已知:如图1,
 中,D、E分别是AB、AC的中点.
中,D、E分别是AB、AC的中点.求证:
 ,
, .
.证明:如图1,延长DE到点F,使得
 ,连接CF;
,连接CF;请继续完成证明过程;

(2)(问题解决)
如图2,在矩形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若
 ,
, ,
, ,求GF的长.
,求GF的长.(3)(思维拓展)
如图3,在梯形ABCD中,
 ,
, ,
, ,E为AD的中点,G、F分别为AB、CD边上的点,若
,E为AD的中点,G、F分别为AB、CD边上的点,若 ,
, ,
, ,求GF的长.
,求GF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是BC边的中点,将△ABE沿AE所在直线折叠得到△AGE,延长AG交CD于点F,已知CF=2,FD=1,则BC的长是( )
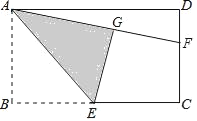
A.3
 B.2
B.2 C.2
C.2 D.2
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】补全下面的解题过程:
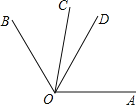
如图,已知OC是∠AOB内部的一条射线,OD是∠AOB的平分线,∠AOC=2∠BOC且∠BOC=40°,求∠COD的度数.
解:因为∠AOC=2∠BOC,∠BOC=40°,所以∠AOC=_____°,所以∠AOB=∠AOC+∠_____=_____°.
因为OD平分∠AOB,所以∠AOD=
 ∠_____=_____°,所以∠COD=∠_____﹣∠AOD=_____°.
∠_____=_____°,所以∠COD=∠_____﹣∠AOD=_____°.
相关试题

