【题目】已知线段![]() 和
和![]() 在同一直线上,如果
在同一直线上,如果![]() ,
,![]() ,则线段
,则线段![]() 和
和![]() 的中点之间的距离为______________
的中点之间的距离为______________![]() .
.
参考答案:
【答案】4 cm或1.6 cm.
【解析】
此题有两种情况:①当C点在线段AB上,此时AB=AC+BC,然后根据中点的性质即可求出线段AC和BC的中点之间的距离;②当B在线段AC上时,那么AB=AC-CB,然后根据中点的性质即可求出线段AC和BC的中点之间的距离.
解:此题有两种情况:
①当C点在线段AB上,此时AB=AC+BC,
而AC=5.6cm,BC=2.4cm,
∴AB=AC+BC=8cm,
∴线段AC和BC的中点之间的距离为![]() cm;
cm;
②当B点在线段AC上,此时AB=AC-BC,
而AC=5.6cm,BC=2.4cm,
∴AB=AC-BC=2.8cm,
∴线段AC和BC的中点之间的距离为![]() cm.
cm.
故答案为:4 cm或1.6 cm.
-
科目: 来源: 题型:
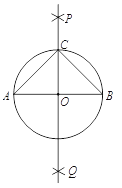
查看答案和解析>>【题目】下面是“作以已知线段为斜边的等腰直角三角形”的尺规作图过程.
已知:线段
 .
.

求作:以
 为斜边的一个等腰直角三角形
为斜边的一个等腰直角三角形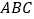 .
.作法:如图,
(1)分别以点
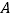 和点
和点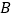 为圆心,大于
为圆心,大于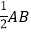 的长为半径作弧,两弧相交于
的长为半径作弧,两弧相交于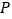 ,
, 两点;
两点;(2)作直线
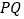 ,交
,交 于点
于点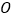 ;
;(3)以
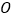 为圆心,
为圆心,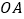 的长为半径作圆,交直线
的长为半径作圆,交直线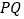 于点
于点 ;
;(4)连接
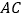 ,
,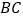 .
.则
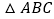 即为所求作的三角形.
即为所求作的三角形.请回答:在上面的作图过程中,①
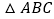 是直角三角形的依据是________;②
是直角三角形的依据是________;②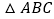 是等腰三角形的依据是__________.
是等腰三角形的依据是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
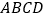 中,
中,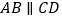 ,
, 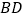 交
交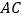 于
于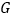 ,
,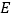 是
是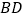 的中点,连接
的中点,连接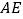 并延长,交
并延长,交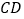 于点
于点 ,
, 恰好是
恰好是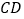 的中点.
的中点.(1)求
 的值;
的值;(2)若
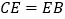 ,求证:四边形
,求证:四边形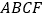 是矩形.
是矩形. 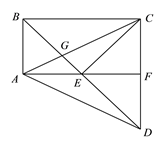
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数
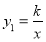 的图像与一次函数
的图像与一次函数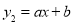 的图像相交于点
的图像相交于点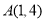 、
、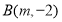 .
.
(1)求出反比例函数和一次函数的关系式;
(2)观察图像,直接写出使得
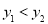 成立的自变量x的取值范围;
成立的自变量x的取值范围;(3)如果点C与点A关于x轴对称,求
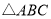 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司购买了一批A、B两种型号的产品,其中A型产品的单价比B型产品的单价多6元,已知该公司用1400元购买A型产品的件数与用1160元购买B型产品的件数相等.
(1)求该公司购买的A、B两种型号产品的单价各是多少元?
(2)若两种型号的产品共购买了100件,且购买的总费用为3260元,求购买了多少件A型产品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】简单多面体是各个面都是多边形组成的几何体,十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)和棱数(E)之间存在一个有趣的关系式,称为欧拉公式.如表是根据左边的多面体模型列出的不完整的表:
多面体
顶点数
面数
棱数
四面体
4
4
6
长方体
8
6
正八面体
8
12
现在有一个多面体,它的每一个面都是三角形,它的面数(F)和棱数(E)的和为30,则这个多面体的顶点数V=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形ABC中,
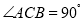 ,
,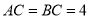 ,D是AB的中点,E、F分别是AC、BC上的点(点E不与端点A、C重合),连接EF并取EF的中点O,连接DO并延长至点G,使
,D是AB的中点,E、F分别是AC、BC上的点(点E不与端点A、C重合),连接EF并取EF的中点O,连接DO并延长至点G,使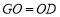 ,连接DE、GE、GF.
,连接DE、GE、GF.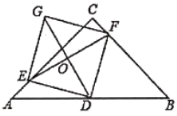
(1)求证:四边形EDFG是平行四边形;
(2)若
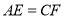 ,探究四边形EDFG的形状?
,探究四边形EDFG的形状?(3)在(2)的条件下,当E点在何处时,四边形EDFG的面积最小,并求出最小值.
相关试题

