【题目】补全下面的解题过程:
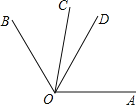
如图,已知OC是∠AOB内部的一条射线,OD是∠AOB的平分线,∠AOC=2∠BOC且∠BOC=40°,求∠COD的度数.
解:因为∠AOC=2∠BOC,∠BOC=40°,所以∠AOC=_____°,所以∠AOB=∠AOC+∠_____=_____°.
因为OD平分∠AOB,所以∠AOD=![]() ∠_____=_____°,所以∠COD=∠_____﹣∠AOD=_____°.
∠_____=_____°,所以∠COD=∠_____﹣∠AOD=_____°.
参考答案:
【答案】80 BOC 120 AOB 60 AOC 20
【解析】
直接利用已知条件并结合角平分线的定义进而分析得出答案.
解:∵∠AOC=2∠BOC,∠BOC=40°.
∴∠AOC=80°.
∴∠AOB=∠AOC+∠BOC=120°.
∵OD平分∠AOB.
∴∠AOD=![]() ∠AOB=60°.
∠AOB=60°.
∴∠COD=∠AOC﹣∠AOD=20°.
故答案为:80,BOC,120,AOB,60,AOC,20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形ABC中,
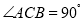 ,
,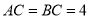 ,D是AB的中点,E、F分别是AC、BC上的点(点E不与端点A、C重合),连接EF并取EF的中点O,连接DO并延长至点G,使
,D是AB的中点,E、F分别是AC、BC上的点(点E不与端点A、C重合),连接EF并取EF的中点O,连接DO并延长至点G,使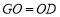 ,连接DE、GE、GF.
,连接DE、GE、GF.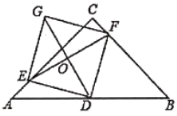
(1)求证:四边形EDFG是平行四边形;
(2)若
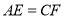 ,探究四边形EDFG的形状?
,探究四边形EDFG的形状?(3)在(2)的条件下,当E点在何处时,四边形EDFG的面积最小,并求出最小值.
-
科目: 来源: 题型:
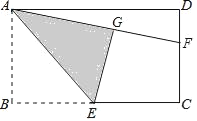
查看答案和解析>>【题目】(1)(方法回顾)证明:三角形中位线定理.
已知:如图1,
 中,D、E分别是AB、AC的中点.
中,D、E分别是AB、AC的中点.求证:
 ,
, .
.证明:如图1,延长DE到点F,使得
 ,连接CF;
,连接CF;请继续完成证明过程;

(2)(问题解决)
如图2,在矩形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若
 ,
, ,
, ,求GF的长.
,求GF的长.(3)(思维拓展)
如图3,在梯形ABCD中,
 ,
, ,
, ,E为AD的中点,G、F分别为AB、CD边上的点,若
,E为AD的中点,G、F分别为AB、CD边上的点,若 ,
, ,
, ,求GF的长.
,求GF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是BC边的中点,将△ABE沿AE所在直线折叠得到△AGE,延长AG交CD于点F,已知CF=2,FD=1,则BC的长是( )
A.3
 B.2
B.2 C.2
C.2 D.2
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】一副三角板的两块三角板的三个角度数分别为90°、60°、30°和90°、45°、45°,我们可以用三角板的角拼出一些特殊度数的角.
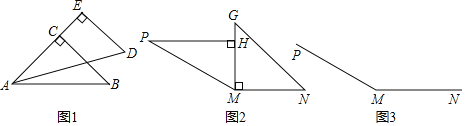
(1)两块三角板按如图1所示拼接,则∠BAD的度数是 °.
(2)小明用两块三角板按图2拼出的∠PMN的度数是 °.
(3)小明想画出图2拼出的∠PMN的角平分线,请你只用一副三角板在图3中帮小明完成画图.(不写画法,保留画图痕迹,标出必要的度数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
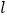 过点
过点 ,且与函数
,且与函数 的图象相交于
的图象相交于 两点,与
两点,与 轴、
轴、 轴分别交于点
轴分别交于点 ,如图所示,四边形
,如图所示,四边形 均为矩形,且矩形
均为矩形,且矩形 的面积为
的面积为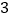 .
.(1)求
 的值;
的值;(2)当点
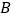 的横坐标为
的横坐标为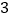 时,求直线
时,求直线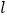 的解析式及线段
的解析式及线段 的长;
的长;(3)如图是小芳同学对线段
 的长度关系的思考示意图.记点
的长度关系的思考示意图.记点 的横坐标为
的横坐标为 ,已知当
,已知当 时,线段
时,线段 的长随
的长随 的增大而减小,请你参考小芳的示意图判断:当
的增大而减小,请你参考小芳的示意图判断:当 时,线段
时,线段 的长随
的长随 的增大而 . (填“增大”、“减小”或“不变”)
的增大而 . (填“增大”、“减小”或“不变”)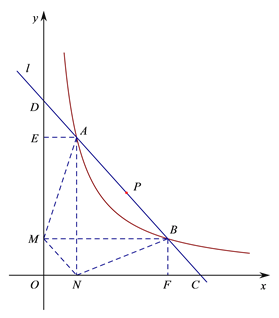
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是甲、乙两名射击运动员的10次射击测试成绩的折线统计图.
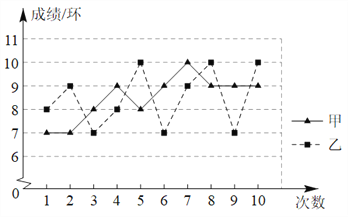
(1)根据折线图把下列表格补充完整;
运动员
平均数
中位数
众数
甲
8.5
9
乙
8.5
(2)根据上述图表运用所学统计知识对甲、乙两名运动员的射击水平进行评价并说明理由.
相关试题

