【题目】如图,![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 在⊙
在⊙![]() 上,
上,![]() 平分
平分![]() ,
,![]() 是⊙
是⊙![]() 的切线,
的切线,![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.

参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1))设∠BAD=α,由于AD平分∠BAC,所以∠CAD=∠BAD=α,进而求出∠D=∠BED=90°﹣α,从而可知BD=BE;
(2)设CE=x,由于AB是⊙O的直径,∠AFB=90°,又因为BD=BE,DE=2,FE=FD=1,由于BD=![]() ,所以tanα=
,所以tanα=![]() ,从而可求出AB=
,从而可求出AB=![]() ,利用勾股定理列出方程即可求出x的值.
,利用勾股定理列出方程即可求出x的值.
试题解析:(1)设∠BAD=α,
∵AD平分∠BAC,∴∠CAD=∠BAD=α,
∵AB是⊙O的直径,∴∠ACB=90°,∴∠ABC=90°﹣2α,
∵BD是⊙O的切线,∴BD⊥AB,∴∠DBE=2α,∠BED=∠BAD+∠ABC=90°﹣α,
∴∠D=180°﹣∠DBE﹣∠BED=90°﹣α,∴∠D=∠BED,∴BD=BE
(2)设AD交⊙O于点F,CE=x,则AC=2x,连接BF,
∵AB是⊙O的直径,∴∠AFB=90°,
∵BD=BE,DE=2,∴FE=FD=1,
∵BD=![]() ,∴tanα=
,∴tanα=![]() ,∴AB=
,∴AB=![]() .
.
在Rt△ABC中,由勾股定理可知:![]() ,
,
∴解得:x=﹣![]() 或x=
或x=![]() ,∴CE=
,∴CE=![]() ;
;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形
 的对角线
的对角线 相交于点
相交于点 ,
, ,
, ,
, ,
, .
.(1)填空:
 与
与 的数量关系为 ;
的数量关系为 ;(2)求
 的值;
的值;(3)将
 沿
沿 翻折,得到
翻折,得到 (如图2),连接
(如图2),连接 ,与
,与 相交于点
相交于点 .若
.若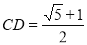 ,求
,求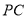 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,H为BC上一点,且BH=BA交AC于点F,连接FH.
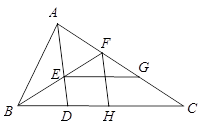
(1)求证:AE=FH;
(2)作EG//BC交AC于点G若AG=5,AC=8,求FG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形一边长为2,另一边长为5,那么这个等腰三角形的周长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,双曲线
中,双曲线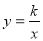 经过□
经过□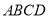 的顶点
的顶点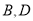 .点
.点 的坐标为
的坐标为 ,点
,点 在
在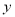 轴上,且
轴上,且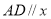 轴,
轴,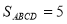 .
.(1)填空:点
 的坐标为 ;
的坐标为 ;(2)求双曲线和
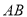 所在直线的解析式.
所在直线的解析式.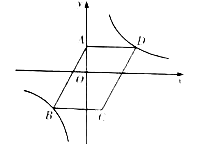
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的原价为100元,如果经过两次降价,且每次降价的百分率都是m,那么该商品现在的价格是_____元(结果用含m的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)已知:如图1,等腰直角三角形ABC中,∠B=90°,AD是∠BAC的外角平分线,交CB边的延长线于点D.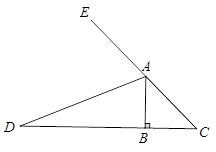
图1
求证:BD=AB+AC
(2)对于任意三角形ABC,∠ABC=2∠C,AD是∠BAC的外角平分线,交CB边的延长线于点D,如图2,请你写出线段AC、AB、BD之间的数量关系并加以证明.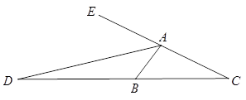
相关试题

