【题目】
(1)已知:如图1,等腰直角三角形ABC中,∠B=90°,AD是∠BAC的外角平分线,交CB边的延长线于点D.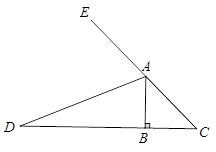
图1
求证:BD=AB+AC
(2)对于任意三角形ABC,∠ABC=2∠C,AD是∠BAC的外角平分线,交CB边的延长线于点D,如图2,请你写出线段AC、AB、BD之间的数量关系并加以证明.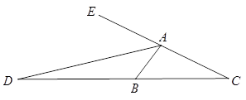
参考答案:
【答案】
(1)解:在AE于上截取AF=AB,连接DF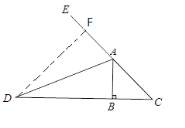
∵AD是∠BAC的外角平分线
∴∠DAF=∠DAB
在△ADF和△ADB中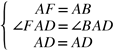
∴△ADF≌△ADB
BD=DF;∠DFA=∠DBA=90°
又∵等腰直角三角形ABC中,∠BAC=∠C=45°
∴FAD=135°
∴∵FDC=45°=∠C
∴DF=FC
∴BD=CF=AC+AF
BD=AB+AC
(2)解:DB=AB+AC理由如下:
在AE上截取AF=AB,连接DF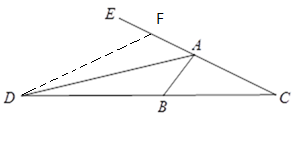
∵AD是∠BAC的外角平分线
∴∠FAD=∠BAD
在△FAD和△BAD中,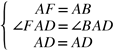
∴△FAD≌△BAD
∠ADF=∠ADB;BD=DF
∠AFD+∠EFD=∠ABD+∠ABC=180°
∴∠EFD=∠ABC
∵∠ABC=2∠C
∴∠EFD=2∠C
∵∠EFD=∠FDC+∠C
∴DF=CF
BD=CF=AF+AC
∴DB=AB+AC
【解析】(1)做辅助线,由外角平分线易得△ADF≌△ADB,再由等腰直角三角形性质易得DF=FC=BD,最终得证DB=AB+AC;
(2)类比(1)中的方法,在证DF=CF时利用所给条件∠ABC=2∠C,可证,最终得证DB=AB+AC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是⊙
是⊙ 的直径,点
的直径,点 在⊙
在⊙ 上,
上, 平分
平分 ,
, 是⊙
是⊙ 的切线,
的切线, 与
与 相交于点
相交于点 .
.(1)求证:
 ;
;(2)若
 ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,双曲线
中,双曲线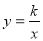 经过□
经过□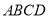 的顶点
的顶点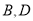 .点
.点 的坐标为
的坐标为 ,点
,点 在
在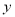 轴上,且
轴上,且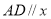 轴,
轴,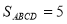 .
.(1)填空:点
 的坐标为 ;
的坐标为 ;(2)求双曲线和
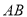 所在直线的解析式.
所在直线的解析式.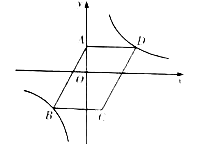
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的原价为100元,如果经过两次降价,且每次降价的百分率都是m,那么该商品现在的价格是_____元(结果用含m的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:4a2﹣25b2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式x2+mx+25能用完全平方公式分解因式,则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目.以下是根据调查结果绘制的统计图表的一部分.
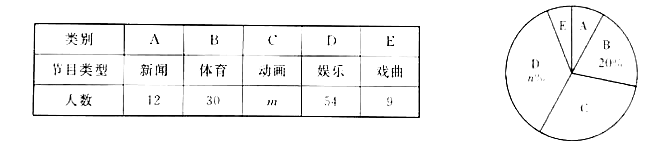
根据以上信息,解答下列问题:
(1)被调查的学生中,最喜爱体育节目的有 人,这些学生数占被调查总人数的百分比为 %;
(2)被调查学生的总数为 人,统计表中
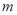 的值为 ,统计图中
的值为 ,统计图中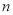 的值为 ;
的值为 ;(3)在统计图中,
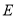 类所对应扇形圆心角的度数为 ;
类所对应扇形圆心角的度数为 ;(4)该校共有2000名学生,根据调查结果,估计该校最喜爱欣慰节目的学生数.
相关试题

