【题目】如图1,四边形![]() 的对角线
的对角线![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)填空:![]() 与
与![]() 的数量关系为 ;
的数量关系为 ;
(2)求![]() 的值;
的值;
(3)将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() (如图2),连接
(如图2),连接![]() ,与
,与![]() 相交于点
相交于点![]() .若
.若![]() ,求
,求![]() 的长.
的长.

参考答案:
【答案】(1)∠BAD+∠ACB=180°;(2)![]() ;(3)1.
;(3)1.
【解析】
试题分析:(1)在△ABD中,根据三角形的内角和定理即可得出结论:∠BAD+∠ACB=180°;
(2)如图1中,作DE∥AB交AC于E.由△OAB≌△OED,可得AB=DE,OA=OE,设AB=DE=CE=CE=x,OA=OE=y,由△EAD∽△ABC,推出![]() ,可得
,可得![]() ,可得4y2+2xy﹣x2=0,即
,可得4y2+2xy﹣x2=0,即![]() ,求出
,求出![]() 的值即可解决问题;
的值即可解决问题;
(3)如图2中,作DE∥AB交AC于E.想办法证明△PA′D∽△PBC,可得![]() ,可得
,可得![]() ,即
,即![]() ,由此即可解决问题;
,由此即可解决问题;
试题解析:(1)如图1中,
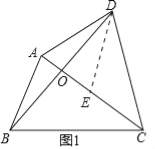
在△ABD中,∵∠BAD+∠ABD+∠ADB=180°,∠ABD+∠ADB=∠ACB,
∴∠BAD+∠ACB=180°,故答案为∠BAD+∠ACB=180°.
(2)如图1中,作DE∥AB交AC于E.
∴∠DEA=∠BAE,∠OBA=∠ODE,
∵OB=OD,∴△OAB≌△OED,
∴AB=DE,OA=OE,设AB=DE=CE=CE=x,OA=OE=y,
∵∠EDA+∠DAB=180°,∠BAD+∠ACB=180°,
∴∠EDA=∠ACB,∵∠DEA=∠CAB,∴△EAD∽△ABC,
∴![]() ,∴
,∴![]() ,
,
∴4y2+2xy﹣x2=0,∴![]() ,
,
∴![]() (负根已经舍弃),∴
(负根已经舍弃),∴![]() .
.
(3)如图2中,作DE∥AB交AC于E.
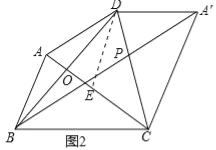
由(1)可知,DE=CE,∠DCA=∠DCA′,∴∠EDC=∠ECD=∠DCA′,
∴DE∥CA′∥AB,∴∠ABC+∠A′CB=180°,
∵△EAD∽△ACB,∴∠DAE=∠ABC=∠DA′C,
∴∠DA′C+∠A′CB=180°,∴A′D∥BC,
∴△PA′D∽△PBC,
∴![]() ,
,
∴![]() ,即
,即![]()
∴PC=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC的顶点分别为A(-4, 5),B(﹣3, 2),C(4,-1).
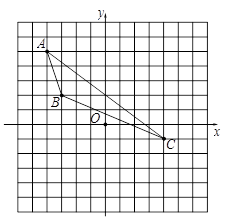
(1)作出△ABC关于x轴对称的图形△A1B1C1;
(2)写出A1、B1、C1的坐标;
(3)若AC=10,求△ABC的AC边上的高. -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式a>0表示的意义是( )
A.a不是负数B.a是负数C.a是非负数D.a是正数
-
科目: 来源: 题型:
查看答案和解析>>【题目】现定义运算“★”,对于任意实数a,b,都有a★b=a2﹣a×b+b,如:3★5=32﹣3×5+5,若x★2=10,则实数x的值为( )
A.﹣4或﹣l
B.4或﹣l
C.4或﹣2
D.﹣4或2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,H为BC上一点,且BH=BA交AC于点F,连接FH.
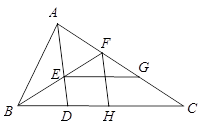
(1)求证:AE=FH;
(2)作EG//BC交AC于点G若AG=5,AC=8,求FG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形一边长为2,另一边长为5,那么这个等腰三角形的周长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是⊙
是⊙ 的直径,点
的直径,点 在⊙
在⊙ 上,
上, 平分
平分 ,
, 是⊙
是⊙ 的切线,
的切线, 与
与 相交于点
相交于点 .
.(1)求证:
 ;
;(2)若
 ,求
,求 的长.
的长.
相关试题

