【题目】如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,H为BC上一点,且BH=BA交AC于点F,连接FH.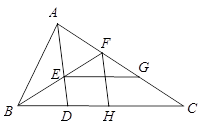
(1)求证:AE=FH;
(2)作EG//BC交AC于点G若AG=5,AC=8,求FG的长.
参考答案:
【答案】
(1)解:∵BE平分∠ABC
∴∠ABF=∠CBF又 ∠BAC=∠ADB
∴∠AFE=∠EDB=∠AEF
∴AE=AF
在△ABF和△ABF中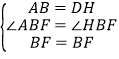
所以△ABF≌△ABF
AF=FH
∴AE=FH
(2)解:由(1)得△ABF≌△ABF
∠AFE=∠EDB=∠AEF=∠BFH
AD∥FH
∴∠FHC=∠ADC
∵EG//BC
∴∠AEG=∠ADC
∴∠FHC=∠AEG;∠AGE=∠C
在△AEG和△FHC中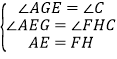
∴△AEG≌△FHC
FC=AG=5
∵AC=8
∴FG=2
【解析】(1)利用角平分线,及对顶角可证△ABF≌△ABF,等量代换可得AE=FH
(2)利用(1)中所给条件及EG//BC,可证△AEG≌△FHC,FC=AG=5,FG=FC+AG-AC=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式a>0表示的意义是( )
A.a不是负数B.a是负数C.a是非负数D.a是正数
-
科目: 来源: 题型:
查看答案和解析>>【题目】现定义运算“★”,对于任意实数a,b,都有a★b=a2﹣a×b+b,如:3★5=32﹣3×5+5,若x★2=10,则实数x的值为( )
A.﹣4或﹣l
B.4或﹣l
C.4或﹣2
D.﹣4或2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形
 的对角线
的对角线 相交于点
相交于点 ,
, ,
, ,
, ,
, .
.(1)填空:
 与
与 的数量关系为 ;
的数量关系为 ;(2)求
 的值;
的值;(3)将
 沿
沿 翻折,得到
翻折,得到 (如图2),连接
(如图2),连接 ,与
,与 相交于点
相交于点 .若
.若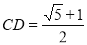 ,求
,求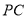 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形一边长为2,另一边长为5,那么这个等腰三角形的周长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是⊙
是⊙ 的直径,点
的直径,点 在⊙
在⊙ 上,
上, 平分
平分 ,
, 是⊙
是⊙ 的切线,
的切线, 与
与 相交于点
相交于点 .
.(1)求证:
 ;
;(2)若
 ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,双曲线
中,双曲线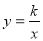 经过□
经过□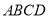 的顶点
的顶点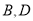 .点
.点 的坐标为
的坐标为 ,点
,点 在
在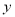 轴上,且
轴上,且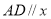 轴,
轴,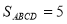 .
.(1)填空:点
 的坐标为 ;
的坐标为 ;(2)求双曲线和
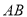 所在直线的解析式.
所在直线的解析式.
相关试题

