【题目】如图,在△ABC中,点D在BC上,∠ADB=∠BAC,BE平分∠ABC,过点E作EF/AD,交BC于点F

(1)求证:∠BAD=∠C;
(2)若∠C=20°,∠BAC=110°,求∠BEF的度数.
参考答案:
【答案】(1)见解析;(2)45°
【解析】
(1)利用三角形内角和证明即可;
(2)利用∠C=20°,∠BAC=110°求出∠ABC,根据BE平分∠ABC求出∠CBE=25°,再根据EF/AD求出∠ADB=∠EFB=110°,最后利用三角形内角和求出结果.
解:(1)∵∠BAD=180°-∠ABC-∠ADB,∠C=180°-∠ABC-∠BAC,
∵∠ADB=∠BAC,
∴∠BAD=∠C;
(2)∵∠C=20°,∠BAC=110°,
∴∠ABC=180°-110°-20°=50°,∠ADB=∠BAC=110°,
∵BE平分∠ABC,
∴∠ABE=∠CBE=25°,
∵AD∥EF,
∴∠ADB=∠EFB=110°,
∴∠BEF=180°-∠CBE-∠BFE=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.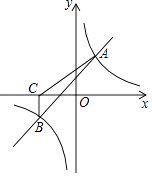
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式kx+b< 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
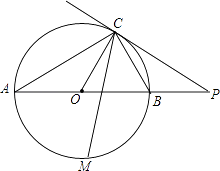
(1)求证:PC是⊙O的切线;
(2)求证:BC= AB;
AB;
(3)点M是 的中点,CM交AB于点N,若AB=4,求MNMC的值.
的中点,CM交AB于点N,若AB=4,求MNMC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
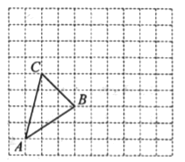
(1)画出△ABC先向右平移5个单位长度,再向上平移2个单位长度所得的△A1B1C1;
(2)画出△ABC的中线AD;
(3)画出△ABC的高CE所在直线,标出垂足E:
(4)在(1)的条件下,线段AA1和CC1的关系是
-
科目: 来源: 题型:
查看答案和解析>>【题目】课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),∠ACB=90°,AC=BC,小明量出AB=26cm,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为________cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,有A型、B型正方形卡片和C型长方形卡片各若干张.

(1)用1张A型卡片,1张B型卡片,2张C型卡片拼成一个正方形,如图2,用两种方法计算这个正方形面积,可以得到一个等式,请你写出这个等式____;
(2)选取1张A型卡片,10张C型卡片,____张B型卡片,可以拼成一个正方形,这个正方形的边长用含a,b的代数式表示为____;
(3)如图3,两个正方形边长分别为m、n,m+n=10,mn=19,求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=4cm,AD=6cm,延长AB到E,使BE=2AB,连接CE,动点F从A出发以2cm/s的速度沿AE方向向点E运动,动点G从E点出发,以3cm/s的速度沿E→C→D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止,设动点运动的时间为t秒.

(1)当t为何值时,FC与EG互相平分;
(2)连接FG,当t<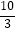 时,是否存在时间t使△EFG与△EBC相似?若存在,求出t的值;若不存在,请说明理由.
时,是否存在时间t使△EFG与△EBC相似?若存在,求出t的值;若不存在,请说明理由.
(3)设△EFG的面积为y,求出y与t的函数关系式,求当t为何值时,y有最大值?最大值是多少?
相关试题

