【题目】如图1,有A型、B型正方形卡片和C型长方形卡片各若干张.

(1)用1张A型卡片,1张B型卡片,2张C型卡片拼成一个正方形,如图2,用两种方法计算这个正方形面积,可以得到一个等式,请你写出这个等式____;
(2)选取1张A型卡片,10张C型卡片,____张B型卡片,可以拼成一个正方形,这个正方形的边长用含a,b的代数式表示为____;
(3)如图3,两个正方形边长分别为m、n,m+n=10,mn=19,求阴影部分的面积.
参考答案:
【答案】(1)![]() ;(2)25,
;(2)25,![]() ;(3)阴影部分的面积为
;(3)阴影部分的面积为![]() .
.
【解析】
(1)方法一:先求出这个正方形的边长,再利用正方形的面积公式即可得;方法二:这个正方形的面积等于两个小正方形的面积与两个长方形的面积之和即可得;然后根据方法一与方法二的面积相等可得出所求的等式;
(2)设选取x张B型卡片,根据(1)中的方法二求出拼成的正方形的面积,然后利用完全平方公式即可求出x的值,最后根据正方形的面积公式即可得其边长;
(3)先利用阴影部分的面积等于大正方形的面积减去两个直角三角形的面积求出阴影部分的面积,再利用完全平方公式进行变形,然后将已知等式的值代入求解即可.
(1)方法一:这个正方形的边长为![]() ,则其面积为
,则其面积为![]()
方法二:这个正方形的面积等于两个小正方形的面积与两个长方形的面积之和
则其面积为![]()
因此,可以得到一个等式![]()
故答案为:![]() ;
;
(2)设选取x张B型卡片,x为正整数
由(1)的方法二得:拼成的正方形的面积为![]()
由题意得:![]() 是一个完全平方公式
是一个完全平方公式
则![]()
因此,拼成的正方形的面积为![]()
所以其边长为![]()
故答案为:25,![]() ;
;
(3)阴影部分的面积为![]()
![]()
![]()
则阴影部分的面积为![]()
![]()
![]()
答:阴影部分的面积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
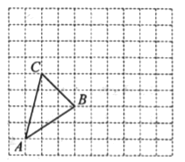
(1)画出△ABC先向右平移5个单位长度,再向上平移2个单位长度所得的△A1B1C1;
(2)画出△ABC的中线AD;
(3)画出△ABC的高CE所在直线,标出垂足E:
(4)在(1)的条件下,线段AA1和CC1的关系是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D在BC上,∠ADB=∠BAC,BE平分∠ABC,过点E作EF/AD,交BC于点F

(1)求证:∠BAD=∠C;
(2)若∠C=20°,∠BAC=110°,求∠BEF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),∠ACB=90°,AC=BC,小明量出AB=26cm,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为________cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=4cm,AD=6cm,延长AB到E,使BE=2AB,连接CE,动点F从A出发以2cm/s的速度沿AE方向向点E运动,动点G从E点出发,以3cm/s的速度沿E→C→D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止,设动点运动的时间为t秒.

(1)当t为何值时,FC与EG互相平分;
(2)连接FG,当t<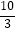 时,是否存在时间t使△EFG与△EBC相似?若存在,求出t的值;若不存在,请说明理由.
时,是否存在时间t使△EFG与△EBC相似?若存在,求出t的值;若不存在,请说明理由.
(3)设△EFG的面积为y,求出y与t的函数关系式,求当t为何值时,y有最大值?最大值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】某集团购买了150吨物资打算运往某地支援,现有甲、乙、丙三种车型供选择,每辆汽车的运载能力和运费如下表所示:(假设每辆车均满载)
车型
甲
乙
丙
汽车运载量(吨/辆)
5
8
10
汽车运费(元/辆)
1000
1200
1500
(1)若全部物资都用甲、乙两种车型来运送,需运费24000元,问分别需甲、乙两种车型各多少辆?
(2)若该集团决定用甲、乙、丙三种汽车共18辆同时参与运送,请你写出可能的运送方案,并帮助该集团找出运费最省的方案(甲、乙、丙三种车辆均要参与运送).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识解决下列问题.

(1)求△ABC的面积;
(2)判断△ABC是什么形状,并说明理由.
相关试题

