搜索
【题目】如图，一次函数y=kx+b与反比例函数y= 
的图象交于A（2，3），B（﹣3，n）两点．
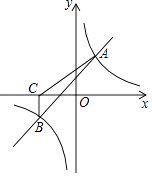
（1）求一次函数与反比例函数的表达式；
（2）根据所给条件，请直接写出不等式kx+b＜ 的解集；
（3）过点B作BC⊥x轴，垂足为C，求S△ABC ．
参考答案：
【答案】
（1）解：∵点A（2，3）在y= 
的图象上，
∴m=6，
∴反比例函数的解析式为：y= 
，
∵B（﹣3，n）在反比例函数图象上，
∴n= 
=﹣2，
∵A（2，3），B（﹣3，﹣2）两点在直线y=kx+b上，
∴ 
解得： 
，
∴一次函数的解析式为：y=x+1；
（2）x＜﹣3或0＜x＜2
（3）解：以BC为底边，则BC边上的高为：|﹣3|+2=5，
∴S△ABC= 
×2×5=5．
【解析】解：（2）由图象得：x＜﹣3或0＜x＜2，
所以答案是：x＜﹣3或0＜x＜2；
-
科目： 来源： 题型：
查看答案和解析>>【题目】若△ABC内有一个点P1，当P1、A、B、C没有任何三点在同一直线上时，如图1，可构成3个互不重叠的小三角形；若△ABC内有两个点P1、P2，其它条件不变，如图2，可构成5个互不重叠的小三角形：……若△ABC内有n个点，其它条件不变，则构成若干个互不重叠的小三角形，这些小三角形的内角和为（）
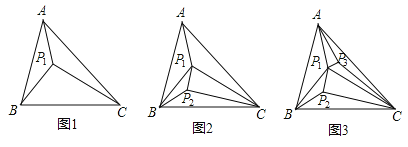
A.n·180°B.（n+2）·180°C.（2n-1）·180°D.（2n+1）·180°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，某校数学兴趣小组为测得大厦AB的高度，在大厦前的平地上选择一点C，测得大厦顶端A的仰角为30°，再向大厦方向前进80米，到达点D处（C，D，B三点在同一直线上），又测得大厦顶端A的仰角为45°，请你计算该大厦的高度．（精确到0.1米，参考数据：
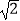≈1.414， 
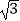≈1.732）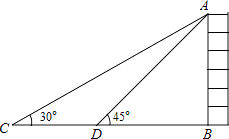
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个不透明的口袋中装有若干个红、黄、蓝、绿四种颜色的小球，小球除颜色外完全相同，为估计该口袋中四种颜色的小球数量，每次从口袋中随机摸出一球记下颜色并放回，重复多次试验，汇总实验结果绘制成如下不完整的条形统计图和扇形统计图．
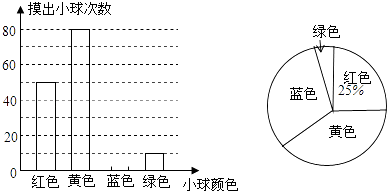
根据以上信息解答下列问题：
（1）求实验总次数，并补全条形统计图；
（2）扇形统计图中，摸到黄色小球次数所在扇形的圆心角度数为多少度？
（3）已知该口袋中有10个红球，请你根据实验结果估计口袋中绿球的数量． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB．
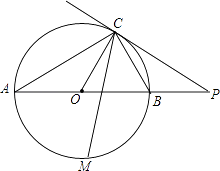
（1）求证：PC是⊙O的切线；
（2）求证：BC=
AB；
（3）点M是
的中点，CM交AB于点N，若AB=4，求MNMC的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】在如图所示的正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的顶点都在正方形网格的格点（网格线的交点）上．
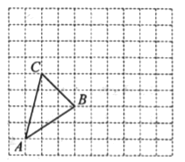
（1）画出△ABC先向右平移5个单位长度，再向上平移2个单位长度所得的△A1B1C1；
（2）画出△ABC的中线AD；
（3）画出△ABC的高CE所在直线，标出垂足E：
（4）在（1）的条件下，线段AA1和CC1的关系是
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，点D在BC上，∠ADB=∠BAC，BE平分∠ABC，过点E作EF/AD，交BC于点F
（1）求证：∠BAD=∠C；
（2）若∠C=20°，∠BAC=110°，求∠BEF的度数．
相关试题
