【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.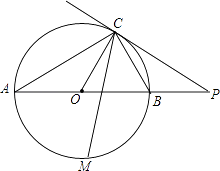
(1)求证:PC是⊙O的切线;
(2)求证:BC= ![]() AB;
AB;
(3)点M是 ![]() 的中点,CM交AB于点N,若AB=4,求MNMC的值.
的中点,CM交AB于点N,若AB=4,求MNMC的值.
参考答案:
【答案】
(1)解:证明:∵OA=OC,
∴∠A=∠ACO.
又∵∠COB=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.
又∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°.
即OC⊥CP,
∵OC是⊙O的半径.
∴PC是⊙O的切线.
(2)解:证明:∵AC=PC,
∴∠A=∠P,
∴∠A=∠ACO=∠PCB=∠P.
又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,
∴BC=OC.
∴BC= ![]() AB.
AB.
(3)解:连接MA,MB,

∵点M是 ![]() 的中点,
的中点,
∴ ![]() ,
,
∴∠ACM=∠BCM.
∵∠ACM=∠ABM,
∴∠BCM=∠ABM.
∵∠BMN=∠BMC,
∴△MBN∽△MCB.
∴ ![]() .
.
∴BM2=MNMC.
又∵AB是⊙O的直径, ![]() ,
,
∴∠AMB=90°,AM=BM.
∵AB=4,
∴BM=2 ![]() .
.
∴MNMC=BM2=8.
【解析】(1)已知点C在圆上,故只需证明OC与PC垂直即可,根据圆周角定理,得∠PCB+∠OCB=90°.即OC⊥CP,故PC是⊙O的切线;(2)AB事直径,故只需证明BC与半径相等即可;(3)连接MA,MB,由圆周角定理可得∠ACM=∠BCM.进而可证△MBN∽△MCB.故BM2=MNMC.代入数据可得MNMC=BM2=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C,D,B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据:
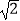 ≈1.414,
≈1.414, 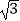 ≈1.732)
≈1.732)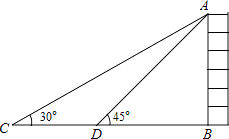
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有若干个红、黄、蓝、绿四种颜色的小球,小球除颜色外完全相同,为估计该口袋中四种颜色的小球数量,每次从口袋中随机摸出一球记下颜色并放回,重复多次试验,汇总实验结果绘制成如下不完整的条形统计图和扇形统计图.
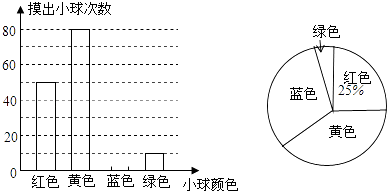
根据以上信息解答下列问题:
(1)求实验总次数,并补全条形统计图;
(2)扇形统计图中,摸到黄色小球次数所在扇形的圆心角度数为多少度?
(3)已知该口袋中有10个红球,请你根据实验结果估计口袋中绿球的数量. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.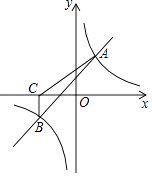
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式kx+b< 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC . -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
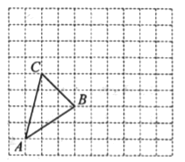
(1)画出△ABC先向右平移5个单位长度,再向上平移2个单位长度所得的△A1B1C1;
(2)画出△ABC的中线AD;
(3)画出△ABC的高CE所在直线,标出垂足E:
(4)在(1)的条件下,线段AA1和CC1的关系是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D在BC上,∠ADB=∠BAC,BE平分∠ABC,过点E作EF/AD,交BC于点F

(1)求证:∠BAD=∠C;
(2)若∠C=20°,∠BAC=110°,求∠BEF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),∠ACB=90°,AC=BC,小明量出AB=26cm,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为________cm.

相关试题

