【题目】陈老师所在的学校为加强学生的体育锻炼,需要购买若干个足球和篮球,他曾两次在某商场购买过足球和篮球,两次购买足球和篮球的数量和费用如下表:
足球数量(个) | 篮球数量(个) | 总费用(元) | |
第一次 | 3 | 5 | 550 |
第二次 | 6 | 7 | 860 |
(1)求足球和篮球的标价;
(2)陈老师计划购买足球a个,篮球b个,可用资金最高为4000元;
①如果计划购买足球和篮球共60个,最多购买篮球多少个?
②如果可用资金恰好全部用完,且购买足球数量不超过篮球数量,则陈老师最多可购买足球________个.
参考答案:
【答案】(1)足球的标价为50元,篮球的标价为80元;(2)①最多购买篮球33个;②24个
【解析】
(1)设足球的标价为x元,篮球的标价为y元,根据图表列出方程组求出x和y的值;
(2)①设购买篮球b个,根据从该商场一次性购买足球和篮球60个,且总费用不能超过4000元,列出不等式求最大正整数解即可;
②设购买足球a个,篮球b个,根据可用资金恰好全部用完,且购买足球数量不超过篮球数量列出不等式,结合a、b均为整数求解即可.
(1)设足球的标价为x元,篮球的标价为y元.根据题意,
可得![]()
解得:![]()
答:足球的标价为50元,篮球的标价为80元;
(2)①根据题意可得
![]()
解得![]() ,
,
因为b为整数,所以![]()
答:最多购买篮球33个
②依题意有:50a+80b=4000且a≤b.
所以b=50- ![]() a≥a,
a≥a,
解得a≤![]() .
.
又b=50- ![]() a是整数,所以a是8的倍数,
a是整数,所以a是8的倍数,
故a最大整数值是24,此时b=35,刚好用完4000元.
答:陈老师最多可购买足球24个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:如图,在△
 中,把
中,把 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转 得到
得到 ,把
,把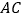 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转 得到
得到 ,连接
,连接 ,当
,当 时,我们称△
时,我们称△ 是△
是△ 的“旋补三角形”,△
的“旋补三角形”,△ 边
边 上的中线
上的中线 叫做
叫做 的“旋补中线”,点
的“旋补中线”,点 叫做“旋补中心”.
叫做“旋补中心”.⑴ 特例感知:在如图、如图中,
 是
是 的“旋补三角形”,
的“旋补三角形”, 是
是 的“旋补中线”.
的“旋补中线”.① 如图,当
 为等边三角形时,
为等边三角形时, 与
与 的数量关系为
的数量关系为 =
=  ;
;② 如图,当
 ,
, 时,则
时,则 长为 .
长为 .⑵ 精确作图:如图,已知在四边形
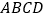 内部存在点
内部存在点 ,使得
,使得 是
是 的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点
的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点 (要求:保留作图痕迹,不写作法和证明)
(要求:保留作图痕迹,不写作法和证明)⑶ 猜想论证:在如图中,当△
 为任意三角形时,猜想
为任意三角形时,猜想 与
与 的数量关系,并给予证明.
的数量关系,并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=2∠B,⊙O的切线AP与OC的延长线相交于点P,若PA= 6
 cm,求AC的长.
cm,求AC的长.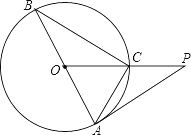
四、综合题(10分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系xOy中的点
 ,若点
,若点 的坐标为
的坐标为 (其中k为常数,且
(其中k为常数,且 ),则称点
),则称点 为点P的“k属派生点”.
为点P的“k属派生点”.例如:
 的“4属派生点”为
的“4属派生点”为 ,即
,即 .
.(1)点
 的“2属派生点”
的“2属派生点” 的坐标为________;
的坐标为________;(2)若点P的“3属派生点”
 的坐标为
的坐标为 ,求点P的坐标;
,求点P的坐标;(3)若点P在y轴的正半轴上,点P的“k属派生点”为
 点,且点
点,且点 到y轴的距离不小于线段OP长度的5倍,则k的取值范围是________________.
到y轴的距离不小于线段OP长度的5倍,则k的取值范围是________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AD是弦,∠A=22.5°,延长AB到点C,使得∠ACD=45°.
(1)求证:CD是⊙O的切线.
(2)若AB=2
 ,求OC的长.
,求OC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求
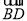 的长(结果保留π).
的长(结果保留π).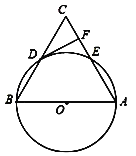
-
科目: 来源: 题型:
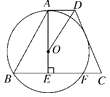
查看答案和解析>>【题目】如图,梯形ABCD中,AD∥BC,AE⊥BC于点E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F.
(1)求证:CD与⊙O相切;
(2)若BF=24,OE=5,求tan∠ABC的值.
相关试题

