【题目】中央电视台举办的“2016年春节联欢晚会”受到广泛关注，某民间组织就2016年春节联欢晚会节目的喜爱程度，在丽州广场进行了问卷调查，并将问卷调查结果分为“非常喜欢”“比较喜欢”“感觉一般”“不太喜欢”四个等级，分别记作A，B，C，D，根据调查结果绘制出如图所示的“扇形统计图”和“条形统计图”，请结合图中所给信息解答下列问题：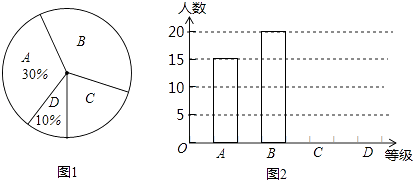
（1）这次被调查对象共有人，被调查者“不太喜欢”有人；
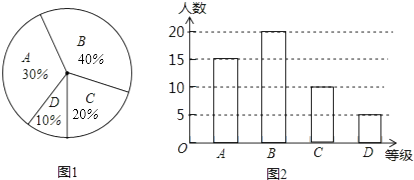
（2）补全扇形统计图和条形统计图；
（3）在“非常喜欢”调查结果里有5人为80后，分别为3男2女，在这5人中，该民间组织打算随机抽取2人进行采访，请你用列表法或列举法求出所选2人均为男生的概率．

参考答案：

【答案】
（1）50；5
（2）解：∵20÷50×100%=40%，

∴1﹣10%﹣30%﹣40%=20%，

∵50×20%=10（人），∴50﹣5﹣10﹣15=20（人），

所求扇形统计图和条形统计图如下图所示：


（3）解：用列表法表示选2人接受采访的所有可能如下：

故：P（所选2人均为男生）=


【解析】解：（1）∵15÷30%=50（人）， ∴50×10%=5（人）
即：这次被调查对象共有 50人，被调查者“不太喜欢”有 5人；
所以答案是：50；5
【考点精析】解答此题的关键在于理解扇形统计图的相关知识，掌握能清楚地表示出各部分在总体中所占的百分比．但是不能清楚地表示出每个项目的具体数目以及事物的变化情况，以及对条形统计图的理解，了解能清楚地表示出每个项目的具体数目，但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况．

关闭