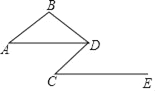
【题目】如图,已知AB∥CD,DA平分∠BDC,∠A=∠C.
(1)试说明:CE∥AD;
(2)若∠C=30°,求∠B的度数.
参考答案:
【答案】(1)详见解析;(2)∠B=120°.
【解析】
(1)欲证明CE∥AD,只需推知∠ADC=∠C即可;
(2)利用(1)中平行线的性质来求∠B的度数.
解:(1)∵AB∥CD,
∴∠A=∠ADC(两直线平行,内错角相等),
∵∠A=∠C,
∴∠ADC=∠C,
∴CE∥AD(内错角相等,两直线平行);
(2)由(1)可得∠ADC=∠C=30°,
∵DA平分∠BDC,∠ADC=∠ADB,
∴∠CDB=2∠ADC=60°,
∵AB∥DC,
∴∠B+∠CDB=180°(两直线平行,同旁内角互补),
∴∠B=180°﹣∠CDB=120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1为某四边形ABCD纸片,其中∠B=70°,∠C=80°.若将CD迭合在AB上,出现折线MN,再将纸片展开后,M、N两点分别在AD、BC上,如图2所示,则∠MNB的度数为何?( )

A.90 B.95 C.100 D.105
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AD、BE、CF分别是三边上的中线.
(1)若AC=1,BC=
 .求证:AD2+CF2=BE2;
.求证:AD2+CF2=BE2;(2)是否存在这样的Rt△ABC,使得它三边上的中线AD、BE、CF的长恰好是一组勾股数?请说明理由.(提示:满足关系a2+b2=c2的3个正整数a、b、c称为勾股数.)

-
科目: 来源: 题型:
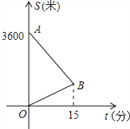
查看答案和解析>>【题目】来自中国、美国、立陶宛、加拿大的四国青年男篮巅峰争霸赛于2014年3月25日-27日在我县体育馆举行。小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.如图中线段AB、OB分别表示父、子俩送票、取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的图象,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(1)从图中可知,小明家离体育馆 米,父子俩在出发后 分钟相遇.
(2)求出父亲与小明相遇时距离体育馆还有多远?
(3)小明能否在比赛开始之前赶回体育馆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,Rt△ABC中,∠ABC=90°,BC<AB<2BC.在AB边上取一点M,使AM=BC,过点A作AE⊥AB且AE=BM,连接EC,再过点A作AN∥EC,交直线CM、CB于点F、N.
(1)证明:∠AFM=45°;
(2)若将题中的条件“BC<AB<2BC”改为“AB>2BC”,其他条件不变,请你在图2的位置上画出图形,(1)中的结论是否仍然成立?如果成立,请说明理由;如果不成立,请猜想∠AFM的度数,并说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42 B.32 C.42 或 32 D.37 或 33
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

相关试题

