搜索
【题目】如图，在Rt△ABC中，∠ACB=90°，AD、BE、CF分别是三边上的中线．
（1）若AC=1，BC=
．求证：AD2+CF2=BE2；
（2）是否存在这样的Rt△ABC，使得它三边上的中线AD、BE、CF的长恰好是一组勾股数？请说明理由．（提示：满足关系a2+b2=c2的3个正整数a、b、c称为勾股数．）
参考答案：
【答案】（1）证明见解析；（2）不存在这样的Rt△ABC，理由见解析.
【解析】试题分析：（1）连接FD，根据三角形中线的定义求出CD、CE，再根据三角形的中位线平行于第三边并且等于第三边的一半可得FD=
AC，然后分别利用勾股定理列式求出AD2、CF2、BE2即可得证；
（2）设两直角边分别为a、b，根据（1）的思路求出AD2、CF2、BE2，再根据勾股定理列出方程表示出a、b的关系，然后用a表示出AD、CF、BE，再进行判断即可．
试题解析：（1）证明：如图，连接FD．∵AD、BE、CF分别是三边上的中线，∴CD=
BC=
，CE=
AC=
，FD=
AC=
，由勾股定理得，AD2=AC2+CD2=12+（
）2=
，CF2=CD2+FD2=（
）2+（
）2=
，BE2=BC2+CE2=（
）2+（
）2=
+
=
，∴AD2+CF2=BE2；
（2）解：设两直角边分别为a、b．∵AD、BE、CF分别是三边上的中线，∴CD=
a，CE=
b，FD=
AC=
a，由勾股定理得，AD2=AC2+CD2=b2+（
a）2=
a2+b2，CF2=CD2+FD2=（
a）2+（
b）2=
a2+
b2，BE2=BC2+CE2=a2+（
b）2=a2+
b2．∵AD2+CF2=BE2，∴
a2+b2+
a2+
b2=a2+
b2，整理得，a2=2b2，∴AD=
b，CF=
b，BE=
b，∴CF：AD：BE=1： 
．∵没有整数是
和
的倍数，∴不存在这样的Rt△ABC．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在等腰直角△ABC的斜边上取异于B，C的两点E，F，使∠EAF=45°，求证：以EF，BE，CF为边的三角形是直角三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知
是Δ
的一个外角，我们容易证明=
，即三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢？尝试探究：
（
）如图2，
与
分别为
的两个外角，则
（横线上填 >、< 或=）初步应用：
（
）如图3，在纸片中剪去
，得到四边形
，
，则
．（
）解决问题：如图4，在中，
、
分别平分外角、，
与
有何数量关系？请利用上面的结论直接写出答案 ．（
）如图5，在四边形
中，
、分别平分外角
、
，请利用上面的结论探究与、
的数量关系．
图1 图2 图3
图4 图5
-
科目： 来源： 题型：
查看答案和解析>>【题目】图1为某四边形ABCD纸片，其中∠B=70°，∠C=80°．若将CD迭合在AB上，出现折线MN，再将纸片展开后，M、N两点分别在AD、BC上，如图2所示，则∠MNB的度数为何？（ ）
A.90 B.95 C.100 D.105
-
科目： 来源： 题型：
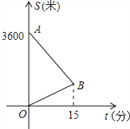
查看答案和解析>>【题目】来自中国、美国、立陶宛、加拿大的四国青年男篮巅峰争霸赛于2014年3月25日-27日在我县体育馆举行。小明来到体育馆看球赛，进场时，发现门票还在家里，此时离比赛开始还有25分钟，于是立即步行回家取票．同时，他父亲从家里出发骑自行车以他3倍的速度给他送票，两人在途中相遇，相遇后小明立即坐父亲的自行车赶回体育馆．如图中线段AB、OB分别表示父、子俩送票、取票过程中，离体育馆的路程S（米）与所用时间t（分钟）之间的图象，结合图象解答下列问题（假设骑自行车和步行的速度始终保持不变）：
（1）从图中可知，小明家离体育馆 米，父子俩在出发后 分钟相遇．
（2）求出父亲与小明相遇时距离体育馆还有多远？
（3）小明能否在比赛开始之前赶回体育馆？
-
科目： 来源： 题型：
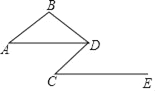
查看答案和解析>>【题目】如图，已知AB∥CD，DA平分∠BDC，∠A=∠C．
（1）试说明：CE∥AD；
（2）若∠C=30°，求∠B的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，Rt△ABC中，∠ABC=90°，BC＜AB＜2BC．在AB边上取一点M，使AM=BC，过点A作AE⊥AB且AE=BM，连接EC，再过点A作AN∥EC，交直线CM、CB于点F、N．
（1）证明：∠AFM=45°；
（2）若将题中的条件“BC＜AB＜2BC”改为“AB＞2BC”，其他条件不变，请你在图2的位置上画出图形，（1）中的结论是否仍然成立？如果成立，请说明理由；如果不成立，请猜想∠AFM的度数，并说明理由．
相关试题
