【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

参考答案:
【答案】(1)证明见解析;(2)70°.
【解析】试题分析:(1)应用“边角边”证得△BDE≌△CEF,所以DE=EF,即△DEF是等腰三角形;
(2)应用角的和差和三角形外角的性质可得∠DEF+∠CEF=∠B+∠BDE ,由△BDE≌△CEF可得∠BDE=∠CEF,进而证得∠DEF=∠B,在△ABC中求得∠B的度数,即可得到∠DEF的度数.
试题解析:(1)证明:∵AB=AC,∴∠B=∠C,
在△BDE和△CEF中:
∵BD=CE,∠B=∠C,BE=CF,
∴△BDE≌△CEF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
(2)解:∵∠DEC=∠B+∠BDE,
即∠DEF+∠CEF=∠B+∠BDE ,
由(1)知△BDE≌△CEF,
则∠BDE=∠CEF,
∴∠DEF=∠B,
∵∠A=40°,
∴∠B=∠C=![]() =70°,
=70°,
∴∠DEF=70°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若4a+3b=1,则8a+6b-3的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有小正方形的边长都为1,A,B,C都在格点上.

(1)过点C画直线AB的平行线(仅利用所给方格纸和直尺作图,下同);
(2)过点A画直线BC的垂线,并注明垂足为G;过点A画直线AB的垂线,交BC于点H.
(3)线段的长度是点A到直线BC的距离;线段AH的长度是点H到直线的距离.
(4)线段AG、AH的大小关系为:AGAH.理由: . -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图。
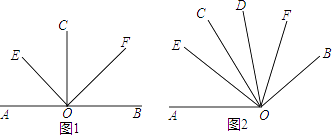
(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;
(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;
(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC= . (用含α与β的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】n边形的外角和是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个数的相反数是负数,那么这个数一定是( ).
A.正数
B.负数
C.零
D.正数、负数、零都有可能 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t<0)秒.
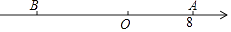
(1)写出数轴上点B表示的数;点P表示的数(用含t的代数式表示)
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P,Q同时出发,问多少秒时P,Q之间的距离恰好等于2?
(3)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速到家动,若点P,Q同时出发,问多少秒时P,Q之间的距离恰好又等于2?
(4)若M为AP的中点,N为BP的中点,在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由,若不变,请他画出图形,并求出线段MN的长.
相关试题

