【题目】△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42 B.32 C.42 或 32 D.37 或 33
参考答案:
【答案】C
【解析】本题考查了勾股定理的应用
当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的周长求出;
(2)当△ABC为钝角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△ABC的周长求出.
此题应分两种情况说明:
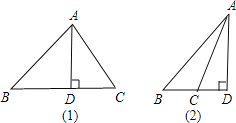
当△ABC为锐角三角形时,
在Rt△ABD中,![]() ,
,
在Rt△ACD中,![]()
∴![]() ,
,
∴△ABC的周长为![]() ;
;
(2)当△ABC为钝角三角形时,
在Rt△ABD中,![]() ,
,
在Rt△ACD中,![]()
∴![]() ,
,
∴△ABC的周长为![]() ;
;
∴当△ABC为锐角三角形时,△ABC的周长为42;当△ABC为钝角三角形时,△ABC的周长为32.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列4个事件:①异号两数相加,和为负数;②异号两数相减,差为正数;③异号两数相乘,积为正数;④异号两数相除,商为负数.必然事件是________,不可能事件是________,随机事件是________.(将事件的序号填上即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于单项式乘法的说法中不正确的是( )
A. 单项式之积不可能是多项式;
B. 单项式必须是同类项才能相乘;
C. 几个单项式相乘,有一个因式为0,积一定为0;
D. 几个单项式的积仍是单项式
-
科目: 来源: 题型:
查看答案和解析>>【题目】著名的瑞士数学家欧拉曾指出:可以表示为四个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为四个整数平方之和,即

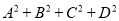 ,这就是著名的欧拉恒等式,有人称这样的数为“不变心的数”.实际上,上述结论可减弱为:可以表示为两个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为两个整数平方之和.
,这就是著名的欧拉恒等式,有人称这样的数为“不变心的数”.实际上,上述结论可减弱为:可以表示为两个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为两个整数平方之和.【动手一试】
试将
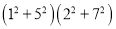 改成两个整数平方之和的形式.
改成两个整数平方之和的形式. 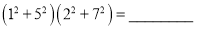 ;
;【阅读思考】
在数学思想中,有种解题技巧称之为“无中生有”.例如问题:将代数式
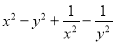 改成两个平方之差的形式.解:原式
改成两个平方之差的形式.解:原式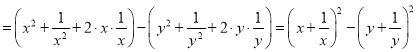 ﹒
﹒【解决问题】
请你灵活运用利用上述思想来解决“不变心的数”问题:将代数式
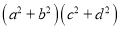 改成两个整数平方之和的形式(其中a、b、c、d均为整数),并给出详细的推导过程﹒
改成两个整数平方之和的形式(其中a、b、c、d均为整数),并给出详细的推导过程﹒ -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法完整且正确的是( )
A. 同底数幂相乘,指数相加; B. 幂的乘方,等于指数相乘;
C. 积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘; D. 单项式乘以单项式,等于系数相乘,同底数幂相乘
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的外接圆的圆心为( )
A. 三条高的交点 B. 三条边的垂直平分线的交点
C. 三条角平分线的交点 D. 三条中线的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的两边长分别为5厘米、9厘米,则这个三角形的周长为.
相关试题

