【题目】如图:在![]() 中,
中,![]() 、
、![]() 分别平分
分别平分![]() 与它的邻补角
与它的邻补角![]() ,
,
![]() 于
于![]() ,
,![]() 于
于![]() ,直线
,直线![]() 分别交
分别交![]() 、
、![]() 于
于![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 为矩形;
为矩形;
![]() 试猜想
试猜想![]() 与
与![]() 的关系,并证明你的猜想;
的关系,并证明你的猜想;
![]() 如果四边形
如果四边形![]() 是菱形,试判断
是菱形,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
参考答案:
【答案】(1)详见解析;(2)![]() 且
且![]() ,证明详见解析;(3)
,证明详见解析;(3)![]() 是直角三角形,证明详见解析.
是直角三角形,证明详见解析.
【解析】
(1)由AE⊥CE于E,AF⊥CF于F可得∠AEC=∠AFC=90°,再由,CE、CF分别平分∠ACB与它的邻补角∠ACD,能证出∠ECF=90°,从而得证.
(2)由矩形的性质可证NE=NC,从而可代换出内错角相等,两直线平行,又因为N是AC的中点,由三角形中位线定理相应的推论可知M是AB的中点.
(3)求出∠ACE=∠EAC=45°,求出AE=CE,根据菱形的判定推出即可.
![]() 证明:∵
证明:∵![]() 于
于![]() ,
,![]() 于
于![]() ,
,
∴![]() ,
,
又∵![]() 、
、![]() 分别平分
分别平分![]() 与它的邻补角
与它的邻补角![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
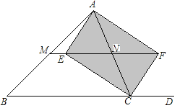
∴三个角为直角的四边形![]() 为矩形;
为矩形;
(2)![]() 且
且![]() ;
;
证明:∵四边形![]() 为矩形,
为矩形,
∴对角线相等且互相平分,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() (矩形的对角线相等且互相平分),
(矩形的对角线相等且互相平分),
∴![]() 是
是![]() 的中位线,
的中位线,
∴![]() ;
;
![]() 解:
解:![]() 是直角三角形
是直角三角形![]() ,
,
理由是:∵![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
∴![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴四边形![]() 是菱形.
是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC是等腰三角形,AB=AC,点D,E,F分别在AB,BC,AC边上,且BD=CE,BE=CF.
(1)求证:△DEF是等腰三角形;
(2)猜想:当∠A满足什么条件时,△DEF是等边三角形?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, ,点
,点 为
为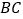 边上一动点,
边上一动点, 于点
于点 ,
, 于点
于点 ,连结
,连结 ,点
,点 为
为 的中点,则
的中点,则 的最小值为________.
的最小值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进甲、乙两种商品,甲种商品共用了
 元,乙种商品共用了
元,乙种商品共用了 元.已知乙种商品每件进价比甲种商品每件进价多
元.已知乙种商品每件进价比甲种商品每件进价多 元,且购进的甲、乙两种商品件数相同.
元,且购进的甲、乙两种商品件数相同. 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价; 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为 元,乙种商品的销售单价为
元,乙种商品的销售单价为 元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的九折销售;乙种商品销售单价保持不变.要使两种商品全部售完后共获利不少于
元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的九折销售;乙种商品销售单价保持不变.要使两种商品全部售完后共获利不少于 元,问甲种商品按原销售单价至少销售多少件?
元,问甲种商品按原销售单价至少销售多少件? -
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读下面材料,然后解决问题:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”.例如:
 ,
, ;当分子的次数小于分母的次数时,我们称之为“真分式”,例如:
;当分子的次数小于分母的次数时,我们称之为“真分式”,例如: ,
, .我们知道,假分数可以化为带分数,例如:
.我们知道,假分数可以化为带分数,例如: =2+
=2+ =2
=2 ,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:
,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如: =1+
=1+ .
.(1)将分式
 化为带分式;
化为带分式;(2)当x取哪些整数值时,分式
 的值也是整数?
的值也是整数? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E.某同学分析图形后得出以下结论:①
 BCD≌
BCD≌ CBE;②
CBE;② BAD≌
BAD≌ BCD;③
BCD;③ BDA≌
BDA≌ CEA;④
CEA;④ BOE≌
BOE≌ COD;⑤
COD;⑤  ACE≌
ACE≌ BCE;上述结论一定正确的是
BCE;上述结论一定正确的是
A. ①②③ B. ②③④ C. ①③⑤ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过四边形
 的四个顶点分别作对角线
的四个顶点分别作对角线 、
、 的平行线,所围成的四边形
的平行线,所围成的四边形 显然是平行四边形.
显然是平行四边形.
 当四边形
当四边形 是分别菱形、矩形时,相应的平行四边形
是分别菱形、矩形时,相应的平行四边形 一定是“菱形、矩形、正方形”中的哪一种?请将你的结论填入下表:
一定是“菱形、矩形、正方形”中的哪一种?请将你的结论填入下表:四边形

菱形
矩形
平行四边形

________
________
 当四边形
当四边形 是矩形时,平行四边形
是矩形时,平行四边形 是什么特殊图形,证明你的结论;
是什么特殊图形,证明你的结论; 反之,当用上述方法所围成的平行四边形是矩形时,相应的原四边形必须满足怎样的条件?(直接写出结论)
反之,当用上述方法所围成的平行四边形是矩形时,相应的原四边形必须满足怎样的条件?(直接写出结论)
相关试题

