【题目】如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E.某同学分析图形后得出以下结论:①![]() BCD≌
BCD≌![]() CBE;②
CBE;②![]() BAD≌
BAD≌![]() BCD;③
BCD;③![]() BDA≌
BDA≌![]() CEA;④
CEA;④![]() BOE≌
BOE≌![]() COD;⑤
COD;⑤ ![]() ACE≌
ACE≌![]() BCE;上述结论一定正确的是
BCE;上述结论一定正确的是

A. ①②③ B. ②③④ C. ①③⑤ D. ①③④
参考答案:
【答案】D
【解析】根据等腰三角形的性质及角平分线定义可得有关角之间的相等关系.运用三角形全等的判定方法AAS或ASA判定全等的三角形.
解:∵AB=AC,∴∠ABC=∠ACB.
∵BD平分∠ABC,CE平分∠ACB,
∴∠ABD=∠CBD=∠ACE=∠BCE.
∴①△BCD≌△CBE (ASA);
③△BDA≌△CEA (ASA);
④△BOE≌△COD (AAS或ASA).
故选D.
此题考查等腰三角形的性质和全等三角形的判定,难度不大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题:
如图,点P在以MN(南北方向)为直径的⊙O上,MN=8,PQ⊥MN交⊙O于点Q,垂足为H,PQ≠MN,弦PC、PD分别交MN于点E、F,且PE=PF.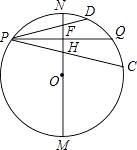
(1)比较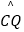 与
与 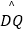 的大小;
的大小;
(2)若OH=2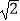 ,求证:OP∥CD;
,求证:OP∥CD;
(3)设直线MN、CD相交所成的锐角为α,试确定cosα=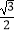 时,点P的位置.
时,点P的位置. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
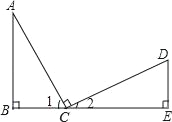
A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△ CED D. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠A=∠C,点P在边AB上.
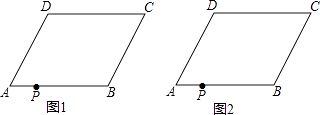
(1)判断四边形ABCD的形状并加以证明;
(2)若AB=AD,以过点P的直线为轴,将四边形ABCD折叠,使点B、C分别落在点B′、C′上,且B′C′经过点D,折痕与四边形的另一交点为Q.
①在图2中作出四边形PB′C′Q(保留作图痕迹,不必说明作法和理由);
②如果∠C=60°,那么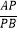 为何值时,B′P⊥AB.
为何值时,B′P⊥AB. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△EFG≌△NMH, ∠F与∠M是对应角.
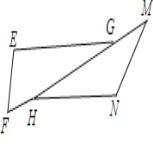
(1)写出相等的线段与相等的角;
(2)若EF=2.1cm,FH=1.1cm,HM=3.3cm,求MN和HG的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BE⊥CD,BE=DE,BC=DA.
求证:(1)△BEC≌△DAE;
(2)DF⊥BC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某市2016年四月每日的最低气温(℃)的统计图,则在四月份每日的最低气温这组数据中,中位数和众数分别是( )

A.14℃,14℃
B.15℃,15℃
C.14℃,15℃
D.15℃,14℃
相关试题

