【题目】如图,过四边形![]() 的四个顶点分别作对角线
的四个顶点分别作对角线![]() 、
、![]() 的平行线,所围成的四边形
的平行线,所围成的四边形![]() 显然是平行四边形.
显然是平行四边形.

![]() 当四边形
当四边形![]() 是分别菱形、矩形时,相应的平行四边形
是分别菱形、矩形时,相应的平行四边形![]() 一定是“菱形、矩形、正方形”中的哪一种?请将你的结论填入下表:
一定是“菱形、矩形、正方形”中的哪一种?请将你的结论填入下表:
四边形 | 菱形 | 矩形 |
平行四边形 | ________ | ________ |
![]() 当四边形
当四边形![]() 是矩形时,平行四边形
是矩形时,平行四边形![]() 是什么特殊图形,证明你的结论;
是什么特殊图形,证明你的结论;
![]() 反之,当用上述方法所围成的平行四边形是矩形时,相应的原四边形必须满足怎样的条件?(直接写出结论)
反之,当用上述方法所围成的平行四边形是矩形时,相应的原四边形必须满足怎样的条件?(直接写出结论)
参考答案:
【答案】(1)矩形,菱形;(2)当四边形![]() 是矩形时,平行四边形
是矩形时,平行四边形![]() 是菱形,理由详见解析;(3)当平行四边形是矩形时,原四边形
是菱形,理由详见解析;(3)当平行四边形是矩形时,原四边形![]() 必须满足的条件是对角线互相垂直.
必须满足的条件是对角线互相垂直.
【解析】
(1)原四边形是菱形时,菱形的对角线互相垂直,因此平行四边形应该是个矩形(平行四边形相邻的两边都垂直),
原四边形是矩形时,它的对角线相等,那么平行四边形应该是个菱形(平行四边形相邻的两边都相等);
(2)根据平行公理的推论求出EF∥GH,EH∥FG,推出平行四边形EFGH,证出邻边相等即可;
(3)根据(1)我们可看出要想使得出的平行四边形是矩形,那么原四边形的对角线就必须垂直,因为只有这样平行四边形的相邻两边才垂直.
(1)四边形ABCD是菱形时,平行四边形EFGH是矩形,
四边形ABCD是矩形时,平行四边形EFGH是菱形,
故答案为:矩形,菱形;
![]() 如图所示:
如图所示:
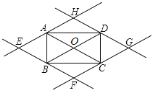
当四边形![]() 是矩形时,平行四边形
是矩形时,平行四边形![]() 是菱形;
是菱形;
理由:∵![]() ,
,![]() .
.
∴四边形![]() ,
,![]() 均为平行四边形,
均为平行四边形,
∵四边形![]() 为矩形,
为矩形,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 为菱形;
为菱形;
![]() 当平行四边形是矩形时,原四边形
当平行四边形是矩形时,原四边形![]() 必须满足的条件是对角线互相垂直.
必须满足的条件是对角线互相垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在
 中,
中, 、
、 分别平分
分别平分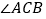 与它的邻补角
与它的邻补角 ,
, 于
于 ,
, 于
于 ,直线
,直线 分别交
分别交 、
、 于
于 、
、 .
.
 求证:四边形
求证:四边形 为矩形;
为矩形;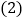 试猜想
试猜想 与
与 的关系,并证明你的猜想;
的关系,并证明你的猜想; 如果四边形
如果四边形 是菱形,试判断
是菱形,试判断 的形状,并说明理由.
的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读下面材料,然后解决问题:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”.例如:
 ,
, ;当分子的次数小于分母的次数时,我们称之为“真分式”,例如:
;当分子的次数小于分母的次数时,我们称之为“真分式”,例如: ,
, .我们知道,假分数可以化为带分数,例如:
.我们知道,假分数可以化为带分数,例如: =2+
=2+ =2
=2 ,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:
,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如: =1+
=1+ .
.(1)将分式
 化为带分式;
化为带分式;(2)当x取哪些整数值时,分式
 的值也是整数?
的值也是整数? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E.某同学分析图形后得出以下结论:①
 BCD≌
BCD≌ CBE;②
CBE;② BAD≌
BAD≌ BCD;③
BCD;③ BDA≌
BDA≌ CEA;④
CEA;④ BOE≌
BOE≌ COD;⑤
COD;⑤  ACE≌
ACE≌ BCE;上述结论一定正确的是
BCE;上述结论一定正确的是
A. ①②③ B. ②③④ C. ①③⑤ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=70°,∠B=90°,点A关于BC的对称点是A',点B关于AC的对称点是B',点C关于AB的对称点是C',若△ABC的面积是1,则△A'B'C'的面积是( )

A.2B.3C.4D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为3的等边△ABC的AB边上任取一点D,作DF⊥AC交AC于F,在BC的延长线上截取CE=AD,连接DE交AC于G,则FG的值为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC

①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
相关试题

