搜索
【题目】如图所示，小正方形方格的边长为 1,
按要求作图，并根据要求解答问题：
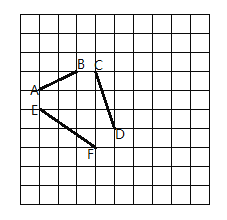
（1）作图：连接图中小正方形方格的某两个顶点，分别得到三条线段
、
、
，使得
、
、
；
（2）判断（1）中的三条线段、、能否构成三角形，并说明理由.
参考答案：
【答案】（1）见解析；（2）能构成三角形，理由见解析．
【解析】
（1）利用网格借助勾股定理得出符合题意的图形；
（2）根据网格结构的特点，过点E、F分别作出与AB、CD相等的线段即可得出结论．
解：（1）∵
=
，
=
，
=
，
∴
是直角边长为1，2的直角三角形的斜边；
是直角边长为1，3的直角三角形的斜边；
是直角边长为2，3的直角三角形的斜边．
如图所示：
（2）能构成三角形，理由如图：
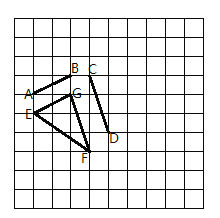
△EFG中，EG=，FG=， ，
∴（1）中的三条线段
、
、
能构成三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，BC＝20 cm，点P，Q，M，N分别从点A，B，C，D出发沿AD，BC，CB，DA方向在矩形的边上同时运动，当有一个点先到达所在运动边的另一个端点时，四个点的运动均停止．已知在相同时间内，若BQ＝x cm(x≠0)，则AP＝2x cm，CM＝3x cm，DN＝x2 cm.
(1)当x为何值时，以PQ，MN为两边，以矩形的边(AD或BC)的一部分为第三边能构成一个三角形？
(2)当x为何值时，以P，Q，M，N为顶点的四边形是平行四边形？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某农场去年种植了10亩地的南瓜，亩产量为2000
，根据市场需要，今年该农场扩大了种植面积，并且全部种植了高产的新品种南瓜，已知南瓜种植面积的增长率是亩产量的增长率的2倍，今年南瓜的总产量为60 000kg，求南瓜亩产量的增长率． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：在△ABC中,∠ABC=60°,CD平分∠ACB交AB于点D,点E在线段CD上(点E不与点C. D重合)，且∠EAC=2∠EBC.
(1)如图1,若∠EBC=27°,且EB=EC,则∠DEB=___°,∠AEC=___°.
(2)如图2，①求证：AE+AC=BC；
②若∠ECB=30°，且AC=BE，求∠EBC的度数。
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：p为实数.
p
k
q
…
…
…
3
16×3＋26
2×2×6
4
16×4＋26
2×3×7
5
16×5＋26
2×4×8
6
16×6＋26
2×5×9
7
16×7＋26
2×6×10
…
…
…
根据上表中的规律，回答下列问题：
(1)当p为何值时，k＝38?
(2)当p为何值时，k与q的值相等？
-
科目： 来源： 题型：
查看答案和解析>>【题目】数学老师在一次“探究性学习”课中，设计了如下数表：
2
3
4
5
…
3
8
15
24
…
4
6
8
10
…
5
10
17
26
…
由表可知，当
时，
，
，
；当
时，
，
，
；………
（1）当
时，
________，
_________，
________. （2）请你分别观察
，，与
之间的关系，并分别用含有的代数式表示 ，，. ________，_________，________. （3）猜想以
，，为边的三角形是否为直角三角形，并说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣6x﹣k2=0（k为常数）．
（1）求证：方程有两个不相等的实数根；
（2）设x1，x2为方程的两个实数根，且x1+2x2=14，试求出方程的两个实数根和k的值．
相关试题
