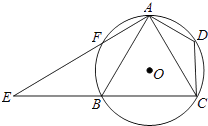
【题目】如图,已知四边形ABCD内接于⊙O,A是 ![]() 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且 ![]() .
. 
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
参考答案:
【答案】
(1)证明:∵四边形ABCD内接于⊙O,
∴∠CDA=∠ABE.
∵ ![]() ,
,
∴∠DCA=∠BAE.
∴△ADC∽△EBA
(2)解:∵A是 ![]() 的中点,
的中点,
∴ ![]()
∴AB=AC=8,
∵△ADC∽△EBA,
∴∠CAD=∠AEC, ![]() ,
,
即 ![]() ,
,
∴AE= ![]() ,
,
∴tan∠CAD=tan∠AEC= ![]() =
= ![]() =
= ![]()
【解析】(1)欲证△ADC∽△EBA,只要证明两个角对应相等就可以.可以转化为证明且 ![]() 就可以;(2)A是
就可以;(2)A是 ![]() 的中点,的中点,则AC=AB=8,根据△CAD∽△ABE得到∠CAD=∠AEC,求得AE,根据正切三角函数的定义就可以求出结论.
的中点,的中点,则AC=AB=8,根据△CAD∽△ABE得到∠CAD=∠AEC,求得AE,根据正切三角函数的定义就可以求出结论.
【考点精析】根据题目的已知条件,利用圆周角定理和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,下列n(n为正整数)个关于x的一元二次方程: ①x2﹣1=0,②x2+x﹣2=0,③x2+2x﹣3=0,④x2+3x﹣4=0,…,,…
(1)上述一元二次方程的解为①________,②________,③________,④________.
(2)猜想:第n个方程为________,其解为________.
(3)请你指出这n个方程的根有什么共同的特点(写出一条即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是18,则DP的长是( )
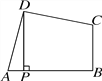
A. 3 B. 2
 C. 3
C. 3 D. 3
D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=
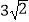 ,CD=
,CD=  ,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为
,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为  ,则满足条件的点P有个.
,则满足条件的点P有个. 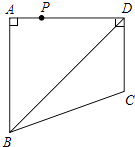
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DB∥AC,且DB=
 AC,E是AC的中点,
AC,E是AC的中点,(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在 △ABC 中,∠C=90°,DB⊥BC 于点 ,分别以点 D 和点 为圆心,以大于
 的长为半径作弧,两弧相交于点 E 和点 ,作直线 EF,延长 AB 于点 ,连接 DG,下面是说明 ∠A=∠D 的说理过程,请把下面的说理过程补充完整:
的长为半径作弧,两弧相交于点 E 和点 ,作直线 EF,延长 AB 于点 ,连接 DG,下面是说明 ∠A=∠D 的说理过程,请把下面的说理过程补充完整:因为 DB⊥BC(已知),
所以 ∠DBC=90°( ) .
因为 ∠C=90°(已知),
所以 ∠DBC=∠C(等量代换),
所以 DB∥AC ( ) ,
所以 (两直线平行,同位角相等);
由作图法可知:直线 EF 是线段 DB 的 ( ) ,
所以 GD=GB,线段 (上的点到线段两端点的距离相等),
所以 ( ) ,因为 ∠A=∠1(已知),
所以 ∠A=∠D(等量代换).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.
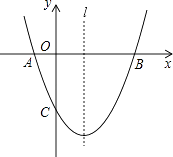
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
相关试题

