【题目】已知,下列n(n为正整数)个关于x的一元二次方程: ①x2﹣1=0,②x2+x﹣2=0,③x2+2x﹣3=0,④x2+3x﹣4=0,…,,…
(1)上述一元二次方程的解为①________,②________,③________,④________.
(2)猜想:第n个方程为________,其解为________.
(3)请你指出这n个方程的根有什么共同的特点(写出一条即可).
参考答案:
【答案】(1)x1=1,x2=﹣1;x1=1,x2=﹣2;x1=1,x2=﹣3;x1=1,x2=﹣4(2)x1=1,x2=﹣n(3)这n个方程都有一个根是1; 另一个根是n的相反数; a+b+c=0; b2﹣4ac=(n+1)2;都有两个不相等的实数根;两个根异号
【解析】试题分析:(1)用十字相乘法因式分解可以求出它们的根.
(2)由(1)找出规律,写出方程,解方程求出方程的根.
(3)根据(1)、(2)可以写出它们的共同特点.
试题解析:(1)①(x+1)(x1)=0,
![]()
②(x+2)(x1)=0,
![]()
③(x+3)(x1)=0,
![]()
④(x+4)(x1)=0,
![]()
(2)由(1)找出规律,可写出第n个方程为:
![]()
(x1)(x+n)=0,
解得![]()
(3)这n个方程都有一个根是1;另一个根是n的相反数;a+b+c=0; ![]() 都有两个不相等的实数根;两个根异号.
都有两个不相等的实数根;两个根异号.
故答案是:(1)①![]() ②
②![]() ③
③![]() ④
④![]()
(2) ![]()
![]()
(3)这n个方程都有一个根是1;另一个根是n的相反数;a+b+c=0; ![]() 都有两个不相等的实数根;两个根异号.
都有两个不相等的实数根;两个根异号.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P与点 Q 都在y轴上,且关于x轴对称.
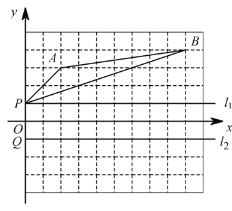
(1)请画出△ABP 关于x轴的对称图形
 (其中点 A 的对称点用
(其中点 A 的对称点用  表示,点 的对称点用
表示,点 的对称点用  表示);
表示);(2)点P ,Q 同时都从y轴上的位置出发,分别沿l1,l2方向,以相同的速度向右运动,在运动过程中是否在某个位置使得

 成立?若存在,请你在图中画出此时 PQ 的位置(用线段
成立?若存在,请你在图中画出此时 PQ 的位置(用线段  表示),若不存在,请你说明理由(注:画图时,先用铅笔画好,再用钢笔描黑).
表示),若不存在,请你说明理由(注:画图时,先用铅笔画好,再用钢笔描黑). -
科目: 来源: 题型:
查看答案和解析>>【题目】从2017年起,昆明将迎来“高铁时代”,这就意味着今后昆明的市民外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从昆明到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:(1)普通列车的行驶路程为________千米;(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(a+c)x2+2bx+a﹣c=0,其中a、b、c分别为△ABC三边的长.下列关于这个方程的解和△ABC形状判断的结论错误的是( )
A. 如果x=﹣1是方程的根,则△ABC是等腰三角形
B. 如果方程有两个相等的实数根,则△ABC是直角三角形
C. 如果△ABC是等边三角形,方程的解是x=0或x=﹣1
D. 如果方程无实数解,则△ABC是锐角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是18,则DP的长是( )
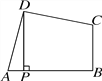
A. 3 B. 2
 C. 3
C. 3 D. 3
D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=
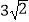 ,CD=
,CD=  ,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为
,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为  ,则满足条件的点P有个.
,则满足条件的点P有个. 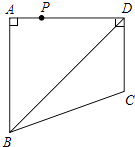
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD内接于⊙O,A是
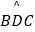 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且 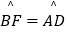 .
. 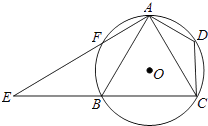
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
相关试题

