【题目】如图,AB是⊙O的直径,弦BC=4㎝,F是弦BC的中点,∠ABC=60°,若动点E以1 ㎝/s的速度从A点出发在AB上沿着A→B→A运动,设运动时间为t(s)(0≤t<16),连接EF,当△BEF是直角三角形时,t(s)的值为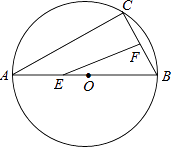
参考答案:
【答案】4.
【解析】根据圆周角定理得到∠C=90°,由于∠ABC=60°,BC=4cm,根据含30度的直角三角形三边的关系得到AB=2BC=8cm,而F是弦BC的中点,所以当EF∥AC时,△BEF是直角三角形,此时E为AB的中点,易得t=4s;当从A点出发运动到B点名,再运动到O点时,此时t=12s;也可以过F点作AB的垂线,点E点运动到垂足时,△BEF是直角三角形.
∵AB是⊙O的直径,
∴∠C=90°,
而∠ABC=60°,BC=4cm,
∴AB=2BC=8cm,
∵F是弦BC的中点,
∴当EF∥AC时,△BEF是直角三角形,
此时E为AB的中点,即AE=AO=4cm,
∴t= ![]() =4.
=4.
【考点精析】本题主要考查了圆周角定理的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,线段
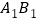 是由线段AB平移得到的,已知A、B两点的坐标分别为A(—2,3),B(—3,1)若
是由线段AB平移得到的,已知A、B两点的坐标分别为A(—2,3),B(—3,1)若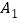 的坐标为(3,4).
的坐标为(3,4).(1)
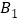 的坐标为 ;
的坐标为 ;(2)若线段AB上一点P的坐标为(
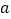 ,
,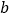 ),则点P的对应点
),则点P的对应点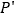 的坐标 .
的坐标 .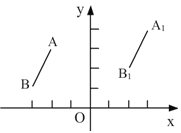
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:有一组对角互补的凸四边形叫做“对补四边形”,性质:“对补四边形”一定是圆内接四边形.
(1)概念理解:请你根据上述描述定义举一个“对补四边形”的例子;
(2)问题探究:如图1,在对补四边形ABCD中,如果∠A=∠C,试探究AB、AD、BC、CD之间的数量关系,并说明理由;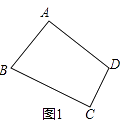
(3)应用拓展:如图2,在四边形ABCD中,AB≠BC,∠A=∠C=90°,连接BD,将△BCD沿BD折叠,得到△BFD.
①连接AF,四边形ABDF是对补四边形吗?请说明理由;
②若AB=1,BD=2,且BF把△ABD分成两个三角形的面积比为1:2,请求出CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等边△ABC所在平面内找出一个点,使它与三角形中的任意两个顶点所组成的三角形都是等腰三角形。这样的点一共有( )
A. 1个 B. 4个 C. 7个 D. 10个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD
(1)求∠AOD的度数;
(2)求证:四边形ABCD是菱形.
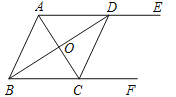
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 在平面直角坐标系中,且
在平面直角坐标系中,且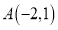 、
、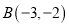 、
、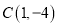 .将其平移后得到
.将其平移后得到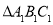 ,若
,若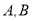 的对应点是
的对应点是 ,
,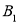 ,
,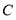 的对应点
的对应点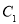 的坐标是
的坐标是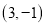 .
.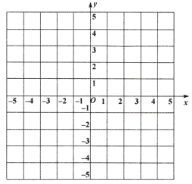
(1)在平面直角坐标系中画出
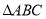 和
和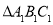 ;
;(2)此次平移也可看作
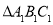 向_________平移________个单位长度,再向__________平移了________个单位长度得到
向_________平移________个单位长度,再向__________平移了________个单位长度得到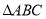 ;
;(3)求
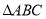 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过原点O的直线与双曲线y=
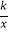 交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( )
交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( ) 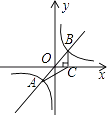
A.
B.
C.5
D.10
相关试题

