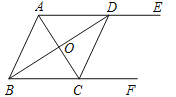
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD
(1)求∠AOD的度数;
(2)求证:四边形ABCD是菱形.
参考答案:
【答案】(1)90°;(2)证明见解析.
【解析】
试题分析:(1)首先根据角平分线的性质得到∠DAC=∠BAC,∠ABD=∠DBC,然后根据平行线的性质得到∠DAB+∠CBA=180°,从而得到∠BAC+∠ABD=![]() (∠DAB+∠ABC)=
(∠DAB+∠ABC)=![]() ×180°=90°,得到答案∠AOD=90°;
×180°=90°,得到答案∠AOD=90°;
(2)根据平行线的性质得出∠ADB=∠DBC,∠DAC=∠BCA,根据角平分线定义得出∠DAC=∠BAC,∠ABD=∠DBC,求出∠BAC=∠ACB,∠ABD=∠ADB,根据等腰三角形的判定得出AB=BC=AD,根据平行四边形的判定得出四边形ABCD是平行四边形,即可得出答案.
试题解析:(1)∵AC、BD分别是∠BAD、∠ABC的平分线,∴∠DAC=∠BAC,∠ABD=∠DBC,∵AE∥BF,∴∠DAB+∠CBA=180°,∴∠BAC+∠ABD=![]() (∠DAB+∠ABC)=
(∠DAB+∠ABC)=![]() ×180°=90°,∴∠AOD=90°;
×180°=90°,∴∠AOD=90°;
(2)证明:∵AE∥BF,∴∠ADB=∠DBC,∠DAC=∠BCA,∵AC、BD分别是∠BAD、∠ABC的平分线,∴∠DAC=∠BAC,∠ABD=∠DBC,∴∠BAC=∠ACB,∠ABD=∠ADB,∴AB=BC,AB=AD
∴AD=BC,∵AD∥BC,∴四边形ABCD是平行四边形,∵AD=AB,∴四边形ABCD是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD的外侧,作等边
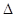 ADE,则
ADE,则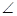 BED的度数是 .
BED的度数是 .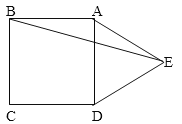
-
科目: 来源: 题型:
查看答案和解析>>【题目】一条东西走向的道路上,小明先向西走3米,记作“﹣3米”,他又向西走了4米,此时小明的位置可记作( )
A. ﹣2米 B. +7米 C. ﹣3米 D. ﹣7米
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC≌△DEF,∠A=80°,∠C=75°则∠E=°
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮根据取x的值为:1.1,1.2,1.3,1.4,1.5时,代入x2﹣12x﹣15求值,估算一元二次方程的解( )
x
1.1
1.2
1.3
1.4
1.5
x2+12x﹣15
﹣.59
0.84
2.29
3.76
5.25
A.1.1<x<1.2
B.1.2<x<1.3
C.1.3<x1.4
D.1.4<x<1.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】抛一枚普通硬币10次,其中4次出现正面,则出现正面的频率为( )
A.2.5
B.1.6
C.0.6
D.0.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】对于两个全等的三角形,下列结论正确的有( )
①两个三角形的周长相等;②两个三角形的面积相等;③两个三角形对应角的平分线相等;④两个三角形对应边上的中线相等
A.1个B.2个C.3个D. 4个
相关试题

