【题目】填写推理的依据。
(1)已知:AB∥CD,AD∥BC。求证:∠B=∠D。
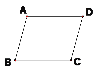
证明:∵AB∥CD,AD∥BC( 已知 )
∴∠A+∠B=180,∠A+∠D=180°(_______________________________)
∴∠B=∠D (___________________________)
(2)已知:DF∥AC,∠A=∠F。求证:AE∥BF。
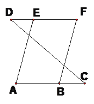
证明:∵DF∥AC (已知)
∴∠FBC=∠_______(_______________________________)
∵∠A=∠F(已知)
∴∠A=∠FBC (____________________)
∴AE∥FB (_____________________________)
参考答案:
【答案】两直线平行,同旁内角互补 等量代换 ∠F, 两直线平行,内错角相等 等量代换 同位角相等,两直线平行
【解析】
(1)根据平行线的特点,两直线平行,同旁内角互补,再根据等量代换即可得出答案,
(2)根据平行线的性质,两直线平行内错角相等,再根据等量代换得出∠A=∠FBC,再根据同位角相等,即可证明两直线平行,
(1)证明:∵AB∥CD,AD∥BC(已知)
∴![]() ,(两直线平行,同旁内角互补)
,(两直线平行,同旁内角互补)
∴∠B=∠D,(等量代换)
(2)证明:∵DF∥AC(已知)
∴∠FBC=∠F,(两直线平行,内错角相等)
∵∠A=∠F(已知)
∴∠A=∠FBC,(等量代换),
∴AE∥FB,(同位角相等,两直线平行)
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学本学期11次考试的测试成绩如下:
甲
98
100
100
90
96
91
89
99
100
100
93
乙
98
99
96
94
95
92
92
98
96
99
97
(1) 他们的平均成绩和方差各是多少?
(2) 分析他们的成绩各有什么特点?
(3) 现要从两人中选一人参加比赛,历届比赛成绩表明,平时成绩达到98分以上才可能进入决赛,你认为应选谁参加这次比赛?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=90
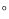 ,射线OC绕点O从OA位置开始,以每秒4
,射线OC绕点O从OA位置开始,以每秒4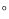 的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1
的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1 的速度逆时针方向旋转. 当OC与OA成180
的速度逆时针方向旋转. 当OC与OA成180 时,OC与OD同时停止旋转.
时,OC与OD同时停止旋转.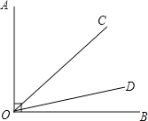
(1)当OC旋转10秒时,∠COD=___.
(2)当OC与OD的夹角是30
 时,求旋转的时间.
时,求旋转的时间.(3)当OB平分∠COD时,求旋转的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC,∠C=90°,∠ABC=40°,按以下步骤作图:
①以点A为圆心,小于AC的长为半径.画弧,分别交AB、AC于点E、F;
②分别以点E、F为圆心,大于
 EF的长为半径画弧,两弧相交于点G;
EF的长为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D,则∠ADC的度数为________.

【答案】65°
【解析】由题意可知,所作的射线AG是∠BAC的角平分线.
∵在△ABC中,∠C=90°,∠ABC=40°,
∴∠BAC=180°-90°-40°=50°,
∴∠CAD=
 ∠BAC=25°,
∠BAC=25°,∴∠ADC=180°-90°-25°=65°.
【题型】填空题
【结束】
13【题目】如图所示,已知线段AB,∠α,∠β,分别过A、B作∠CAB=∠α,∠CBA=∠β.(不写作法,保留作图痕迹)



-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在一次测量旗杆高度的活动中,某小组使用的方案如下:AB表示某同学从眼睛到脚底的距离,CD表示一根标杆,EF表示旗杆,AB、CD、EF都垂直于地面。若AB=1.6m,CD=2m,人与标杆之间的距离BD=1m,标杆与旗杆之间的距离DF=30m,求旗杆EF的高度。
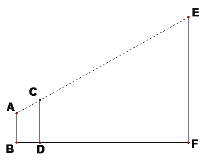
(2)如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6),点C是线段AB的中点。请问在x轴上是否存在一点P,使得以P、A、C为顶点的三角形与△AOB相似?若存在,求出P点坐标(写出计算的过程);若不存在,说明理由。
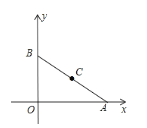
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1=∠2,∠3=∠4,则下面结论中错误的是( )

A. △ADC≌△BCD B. △ABD≌△BAC C. △AOB≌△COD D. △AOD≌△BOC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
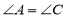 ,
,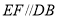 .说明
.说明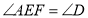 的理由.
的理由.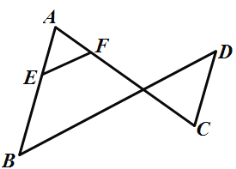
解:∵
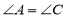 (已知),
(已知),∴________//________(_______________)
∴
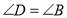 (_______________)
(_______________)∵
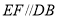 (________),
(________),∴
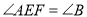 (_______________)
(_______________)∵
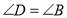 (己证),
(己证),∴
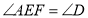 (_______________).
(_______________).
相关试题

