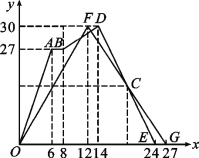
【题目】甲、乙两组同学玩“两人背夹球”比赛,即:每组两名同学用背部夹着球跑完规定的路程,若途中球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果:甲组两位同学掉了球;乙组两位同学顺利跑完.设比赛中同学距出发点的距离用y表示,单位是米;比赛时间用x表示,单位是秒.两组同学比赛过程用图像表示如下:
(1)这是一次 米的背夹球比赛;
(2)线段 表示甲组两位同学在比赛中途掉球,耽误了 秒;
(3)甲组同学到达终点用了 秒,乙组同学到达终点用了 秒,获胜的是 组同学;
(4)请直接写出C点坐标,并说明点C的实际意义.
参考答案:
【答案】(1)60;(2)AB,2;(3)24,27,甲;(4)C的坐标(18,18),点C的实际意义是当比赛进行到18秒时,甲组同学追上乙组同学,此时甲、乙两组同学离终点均为18米.
【解析】
(1)根据函数图象的纵坐标为30,可得这是一次60米的背夹球比赛;
(2)因为从A到B的路程不变,所以甲组两位同学在比赛中掉了球,因为从A到B的时间为2秒,所以耽误了2秒;
(3)利用横坐标可得,甲组同学用了24秒,乙组同学用了27秒,获胜的是甲组同学;
(4)根据点F,G的坐标,求出直线FG的函数解析式,根据点D,E的坐标,求出直线DE的函数解析式,然后组成方程组,求方程组的解,即为C的坐标,即可解答.
解:(1)根据函数图象可得这是一次60米的背夹球比赛;
(2)因为从A到B的路程不变,所以甲组两位同学在比赛中掉了球,因为从A到B的时间为2秒,所以线段AB表示甲组两位同学在比赛中掉了球,耽误了2秒;
(3)根据横坐标可知,甲组同学到达终点用了24秒,乙组同学到达终点用了27秒,获胜的是甲组同学;
(4)设直线FG的函数解析式为:y=k1x+b1,
把F(12,30),G(27,0)代入y=k1x+b1 得:
![]() ,
,
解得:![]() ,
,
∴直线FG的函数解析式为:y=-2x+54;
设直线DE的函数解析式为:y=k2x+b2,
把D(14,30),E(24,0)代入y=k2x+b2 得:
![]() ,
,
解得:![]() ,
,
∴直线DE的函数解析式为:y=-3x+72,
∴得到方程组![]() ,
,
解得:![]() ,
,
∴C的坐标(18,18),表示当比赛进行到18秒时,甲组同学追上乙组同学,此时甲、乙两组同学离终点均为18米.
故答案为:(1)60;(2)AB,2;(3)24,27,甲;(4)C的坐标(18,18),点C的实际意义是当比赛进行到18秒时,甲组同学追上乙组同学,此时甲、乙两组同学离终点均为18米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王晓同学要证明命题“对角线相等的平行四边形是矩形”是正确的,她先作出了如图所示的平行四边形ABCD,并写出了如下不完整的已知和求证.

已知:如图,在平行四边形ABCD中, .
求证:平行四边形ABCD是 .
(1)在方框中填空,以补全已知和求证;
(2)按王晓的想法写出证明过程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设M(m,n)在反比例函数y=﹣
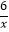 上,其中m是分式方程
上,其中m是分式方程 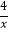 ﹣1=
﹣1= 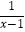 的根,将M点先向上平移4个单位,再向左平移1个单位,得到点N.若点M,N都在直线y=kx+b上,直线解析式为( )
的根,将M点先向上平移4个单位,再向左平移1个单位,得到点N.若点M,N都在直线y=kx+b上,直线解析式为( )
A.y=﹣ x﹣
x﹣ 
B.y= x+
x+ 
C.y=4x﹣5
D.y=﹣4x+5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD满足AB:BC=1:
 ,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )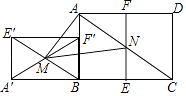
A.4
B.4
C.2
D.1 -
科目: 来源: 题型:
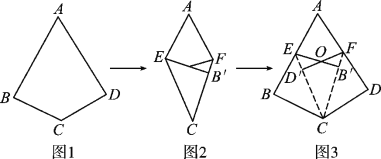
查看答案和解析>>【题目】阅读理解:如图1,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.将一张如图1所示的“完美筝形”纸片ABCD先折叠成如图2所示形状,再展开得到图3,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB′,FD′相交于点O.
简单应用:
(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是 ;
(2)当图3中的∠BCD=120°时,∠AEB′= ;
拓展提升:
(3)当图2中的四边形AECF为菱形时,对应图3中的四边形CD′OB′是否是“完美筝形”?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 的面积是12,点D、E、F、G分别是BC、AD、BE、CE的中点,则四边形AFDG的面积是( )
的面积是12,点D、E、F、G分别是BC、AD、BE、CE的中点,则四边形AFDG的面积是( ) 
A. 4.5B. 5C. 5.5D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC在x轴正半轴上,点A在第一象限,延长AB交y轴负半轴于点D,延长CA到点E,使AE=AC,双曲线y=
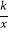 (x>0)的图象过点E.若△BCD的面积为2
(x>0)的图象过点E.若△BCD的面积为2 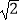 ,则k的值为( )
,则k的值为( )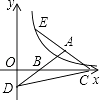
A.4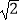
B.4
C.2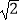
D.2
相关试题

