【题目】设M(m,n)在反比例函数y=﹣ ![]() 上,其中m是分式方程
上,其中m是分式方程 ![]() ﹣1=
﹣1= ![]() 的根,将M点先向上平移4个单位,再向左平移1个单位,得到点N.若点M,N都在直线y=kx+b上,直线解析式为( )
的根,将M点先向上平移4个单位,再向左平移1个单位,得到点N.若点M,N都在直线y=kx+b上,直线解析式为( )
A.y=﹣ ![]() x﹣
x﹣ ![]()
B.y= ![]() x+
x+ ![]()
C.y=4x﹣5
D.y=﹣4x+5
参考答案:
【答案】D
【解析】解:解分式方程 ![]() ﹣1=
﹣1= ![]() 得,x=2,
得,x=2,
∵m是分式方程 ![]() ﹣1=
﹣1= ![]() 的根,
的根,
∴m=2,
∵M(m,n)在反比例函数y=﹣ ![]() 上,
上,
∴n=﹣3,
∴M(2,﹣3),
∵将M点先向上平移4个单位,再向左平移1个单位,得到点N,
∴N(1,1),
∵点M,N都在直线y=kx+b上,
∴ ![]() ,
,
解得 ![]() ,
,
∴直线解析式为:y=﹣4x+5,
所以答案是:D.
【考点精析】本题主要考查了去分母法和确定一次函数的表达式的相关知识点,需要掌握先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊;确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=110°,则∠B的度数是( )
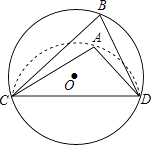
A.110°
B.70°
C.60°
D.55° -
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
阅读理解:数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用较大数与较小数的差来表示.例如:
在数轴上,有理数3与1对应的两点之间的距离为
 ;
;在数轴上,有理数3与-2对应的两点之间的距离为
 ;
;在数轴上,有理数-3与-2对应的两点之间的距离为
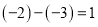 .
.解决问题:如图所示,已知点
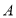 表示的数为-3,点
表示的数为-3,点 表示的数为-1,点
表示的数为-1,点 表示的数为2.
表示的数为2.
(1)点
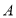 和点
和点 之间的距离为______.
之间的距离为______.(2)若数轴上动点
 表示的数为
表示的数为 ,当
,当 时,点
时,点 和点
和点 之间的距离可表示为______;当
之间的距离可表示为______;当 时,点
时,点 和点
和点 之间的距离可表示为______.
之间的距离可表示为______.(3)若数轴上动点
 表示的数为
表示的数为 ,点
,点 在点
在点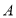 和点
和点 之间,点
之间,点 和点
和点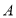 之间的距离表示为
之间的距离表示为 ,点
,点 和点
和点 之间的距离表示为
之间的距离表示为 ,求
,求 (用含
(用含 的代数式表示并进行化简)
的代数式表示并进行化简)(4)若数轴上动点
 表示的数为-2,将点
表示的数为-2,将点 向右移动19个单位长度,再向左移动23个单位长度终点为
向右移动19个单位长度,再向左移动23个单位长度终点为 ,那么
,那么 ,
, 两点之间的距离是______.
两点之间的距离是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】王晓同学要证明命题“对角线相等的平行四边形是矩形”是正确的,她先作出了如图所示的平行四边形ABCD,并写出了如下不完整的已知和求证.

已知:如图,在平行四边形ABCD中, .
求证:平行四边形ABCD是 .
(1)在方框中填空,以补全已知和求证;
(2)按王晓的想法写出证明过程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD满足AB:BC=1:
 ,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )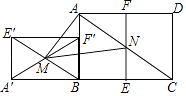
A.4
B.4
C.2
D.1 -
科目: 来源: 题型:
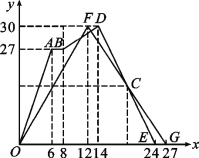
查看答案和解析>>【题目】甲、乙两组同学玩“两人背夹球”比赛,即:每组两名同学用背部夹着球跑完规定的路程,若途中球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果:甲组两位同学掉了球;乙组两位同学顺利跑完.设比赛中同学距出发点的距离用y表示,单位是米;比赛时间用x表示,单位是秒.两组同学比赛过程用图像表示如下:
(1)这是一次 米的背夹球比赛;
(2)线段 表示甲组两位同学在比赛中途掉球,耽误了 秒;
(3)甲组同学到达终点用了 秒,乙组同学到达终点用了 秒,获胜的是 组同学;
(4)请直接写出C点坐标,并说明点C的实际意义.
-
科目: 来源: 题型:
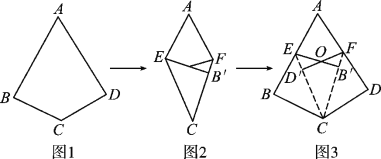
查看答案和解析>>【题目】阅读理解:如图1,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.将一张如图1所示的“完美筝形”纸片ABCD先折叠成如图2所示形状,再展开得到图3,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB′,FD′相交于点O.
简单应用:
(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是 ;
(2)当图3中的∠BCD=120°时,∠AEB′= ;
拓展提升:
(3)当图2中的四边形AECF为菱形时,对应图3中的四边形CD′OB′是否是“完美筝形”?请说明理由.
相关试题

