【题目】王晓同学要证明命题“对角线相等的平行四边形是矩形”是正确的,她先作出了如图所示的平行四边形ABCD,并写出了如下不完整的已知和求证.

已知:如图,在平行四边形ABCD中, .
求证:平行四边形ABCD是 .
(1)在方框中填空,以补全已知和求证;
(2)按王晓的想法写出证明过程.

参考答案:
【答案】(1)AC=BD,矩形;(2)证明详见解析.
【解析】
(1)根据对角线相等的平行四边形是矩形,可得答案;
(2)根据全等三角形的判定与性质,可得∠ADC与∠BCD的关系,根据平行四边形的邻角互补,可得∠ADC的度数,根据矩形的判定,可得答案.
(1)解:在平行四边形ABCD中,AC=BD,求证:平行四边形ABCD是 矩形;
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥CB,AD=BC.
在△ADC和△BCD中,∵AC=BD,AD=BC,CD=DC,
∴△ADC≌△BCD.∴∠ADC=∠BCD.
又∵AD∥CB,
∴∠ADC+∠BCD=180°.
∴∠ADC=∠BCD=90°.
∴平行四边形ABCD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料并完成任务.

莱昂哈德·欧拉是18世纪数学界最杰出的人物之一,瑞士著名的数学家、物理学家,他不但为数学界作出贡献,更把整个数学推至物理的领域;同时,也是数学史上研究成果最多的数学家,平均每年写出八百多页的论文,还写了大量的力学、分析学、几何学等的课本,《无穷小分析引论》《微分学原理》《积分学原理》等都成为数学界中的经典著作.因此,被称为历史上最伟大的两位数学家之一(另一位是卡尔·弗里德里克·高斯).在数学成就上,欧拉最先把关于
 的多项式用记号
的多项式用记号 的形式来表示(
的形式来表示( 可用其他字母代替,但不同的字母表示不同的多项式),例如
可用其他字母代替,但不同的字母表示不同的多项式),例如 ,当
,当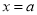 时,多项式的值用
时,多项式的值用 来表示,即
来表示,即 ;当
;当 时,多项式的值用
时,多项式的值用 来表示,记为
来表示,记为 .
.任务:
已知
 ;
; .
.请你根据材料中代入求值的方法解决下列问题:
(1)求
 的值;
的值;(2)求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=110°,则∠B的度数是( )
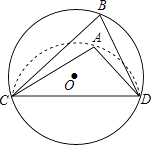
A.110°
B.70°
C.60°
D.55° -
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
阅读理解:数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用较大数与较小数的差来表示.例如:
在数轴上,有理数3与1对应的两点之间的距离为
 ;
;在数轴上,有理数3与-2对应的两点之间的距离为
 ;
;在数轴上,有理数-3与-2对应的两点之间的距离为
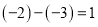 .
.解决问题:如图所示,已知点
 表示的数为-3,点
表示的数为-3,点 表示的数为-1,点
表示的数为-1,点 表示的数为2.
表示的数为2.
(1)点
 和点
和点 之间的距离为______.
之间的距离为______.(2)若数轴上动点
 表示的数为
表示的数为 ,当
,当 时,点
时,点 和点
和点 之间的距离可表示为______;当
之间的距离可表示为______;当 时,点
时,点 和点
和点 之间的距离可表示为______.
之间的距离可表示为______.(3)若数轴上动点
 表示的数为
表示的数为 ,点
,点 在点
在点 和点
和点 之间,点
之间,点 和点
和点 之间的距离表示为
之间的距离表示为 ,点
,点 和点
和点 之间的距离表示为
之间的距离表示为 ,求
,求 (用含
(用含 的代数式表示并进行化简)
的代数式表示并进行化简)(4)若数轴上动点
 表示的数为-2,将点
表示的数为-2,将点 向右移动19个单位长度,再向左移动23个单位长度终点为
向右移动19个单位长度,再向左移动23个单位长度终点为 ,那么
,那么 ,
, 两点之间的距离是______.
两点之间的距离是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】设M(m,n)在反比例函数y=﹣
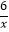 上,其中m是分式方程
上,其中m是分式方程 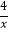 ﹣1=
﹣1= 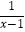 的根,将M点先向上平移4个单位,再向左平移1个单位,得到点N.若点M,N都在直线y=kx+b上,直线解析式为( )
的根,将M点先向上平移4个单位,再向左平移1个单位,得到点N.若点M,N都在直线y=kx+b上,直线解析式为( )
A.y=﹣ x﹣
x﹣ 
B.y= x+
x+ 
C.y=4x﹣5
D.y=﹣4x+5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD满足AB:BC=1:
 ,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )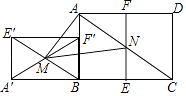
A.4
B.4
C.2
D.1 -
科目: 来源: 题型:
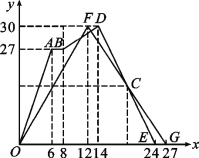
查看答案和解析>>【题目】甲、乙两组同学玩“两人背夹球”比赛,即:每组两名同学用背部夹着球跑完规定的路程,若途中球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果:甲组两位同学掉了球;乙组两位同学顺利跑完.设比赛中同学距出发点的距离用y表示,单位是米;比赛时间用x表示,单位是秒.两组同学比赛过程用图像表示如下:
(1)这是一次 米的背夹球比赛;
(2)线段 表示甲组两位同学在比赛中途掉球,耽误了 秒;
(3)甲组同学到达终点用了 秒,乙组同学到达终点用了 秒,获胜的是 组同学;
(4)请直接写出C点坐标,并说明点C的实际意义.
相关试题

