【题目】如图,四边形ABCD是平行四边形,顶点A、B的坐标分别是A(1,0),B(0,﹣2),顶点C、D在双曲线y=![]() 上,边AD与y轴相交于点E,S四边形BEDC=5S△ABE=10,则k的值是( )
上,边AD与y轴相交于点E,S四边形BEDC=5S△ABE=10,则k的值是( )
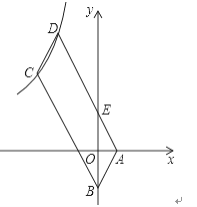
A. -16 B. -9 C. -8 D. -12
参考答案:
【答案】D
【解析】试题解析:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,
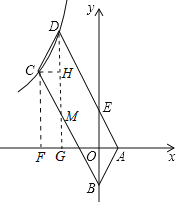
∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
在△CDH和△ABO中,
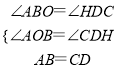 ,
,
∴△CDH≌△ABO(AAS),
∴CH=AO=1,DH=OB=2,
设C(m+1,n),D(m,n+2),
则(m+1)n=m(n+2)=k,
解得n=2m,则D的坐标是(m,2m+2),
设直线AD解析式为y=ax+b,将A、D两点坐标代入得
![]() ,
,
由①得:a=-b,代入②得:mb+b=2m+2,
即b(m+1)=2(m+1),解得b=2,
则![]() ,
,
∴y=-2x+2,
∴E(0,2),BE=4,
∴S△ABE=![]() ×BE×AO=2,
×BE×AO=2,
∵S四边形BCDE=5S△ABE=5×![]() ×4×1=10,
×4×1=10,
∵S四边形BCDE=S△ABE+S四边形BEDM=10,
即2+4×m=10,
解得:m=2,
∴n=2m=4,
∴|k|=(m+1)n=12.
∵双曲线图形在第二象限,
∴k=-12
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF

(1)求证:BF=DC;
(2)求证:四边形ABFD是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF//AD,
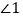 =
=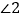 .说明:∠DGA+∠BAC=180°. 填空并写出推理的依据.
.说明:∠DGA+∠BAC=180°. 填空并写出推理的依据.
解:∵EF//AD,(已知)
∴
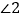 =__ __ (_____________________________)
=__ __ (_____________________________)
又∵
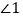 =
=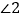 , (已知)
, (已知)∴
 =__ _, (等量替代)
=__ _, (等量替代)∴AB//___ ___, (_______________ _____________)
∴∠DGA+∠BAC=180° (_______________ _________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣1),B(﹣3,3),C(﹣4,1)

(1)画出△ABC关于y轴对称的△A1B1C1 , 并写出点B的对应点B1的坐标;
(2)画出△ABC绕点A按逆时针旋转90°后的△AB2C2 , 并写出点C的对应点C2的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线OB是一次函数y=2x的图象,点A的坐标是(0,2),点C在直线OB上且△ACO为等腰三角形,求C点坐标.
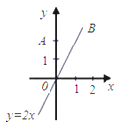
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)列式:x与20的差不小于0;
(2)若(1)中的x(单位:cm)是一个正方形的边长,现将正方形的边长增加2cm,则正方形的面积至少增加多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O—C—B—A—O的路线移动(即:沿着长方形移动一周).
(1)写出点B的坐标( ).
(2)当点P移动了4秒时,请在图中描出此时P点的位置,并求出点P的坐标.
(3)在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.

相关试题

