【题目】如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF 
(1)求证:BF=DC;
(2)求证:四边形ABFD是平行四边形.
参考答案:
【答案】
(1)证明:连接DB,CF,
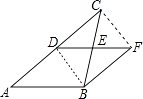
∵DE是△ABC的中位线,
∴CE=BE,
∵EF=ED,
∴四边形CDBF是平行四边形,
∴CD=BF
(2)证明:∵四边形CDBF是平行四边形,
∴CD∥FB,
∴AD∥BF,
∵DE是△ABC的中位线,
∴DE∥AB,
∴DF∥AB,
∴四边形ABFD是平行四边形
【解析】(1)连接DB,CF,利用对角线互相平分的四边形是平行四边形可得四边形CDBF是平行四边形,进而可得CD=BF;(2)由(1)可得CD∥FB,再利用三角形中位线定理可得DF∥AB,根据两组对边分别平行的四边形是平行四边形可得结论.
【考点精析】利用三角形中位线定理和平行四边形的判定对题目进行判断即可得到答案,需要熟知连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
-
科目: 来源: 题型:
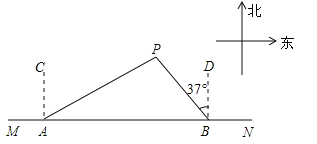
查看答案和解析>>【题目】如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西37°方向上,AP=30海里.
(1)尺规作图:过点P作AB所在直线的垂线,垂足为E(要求:保留作图痕迹,不写作法);
(2)求船P到海岸线MN的距离(即PE的长);
(3)若船A、船B分别以20海里/时、15海里/时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组,并把解集在数轴上表示出来
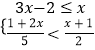 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校体育组对本校九年级全体同学体育测试情况进行调查,他们随机抽查了部分同学体育测试成绩(由高到低分为A、B、C、D四个等级),根据调查的数据绘制成如图的条形统计图和扇形统计图. 请根据以下不完整的统计图提供的信息,解答下列问题:
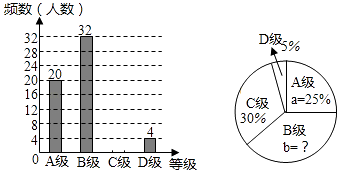
(1)该体育组共抽查了多少名同学的体育测试成绩,扇形统计图中B级所占的百分比b是多少;
(2)补全条形统计图;
(3)若该校九年级共有940名同学,请估计该校九年级同学体育测试达标(测试成绩C级以上,含C级)共多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以正方形ABCD的一边向形外作等边△ABE,BD与EC交于点F,则∠AFD等于( )
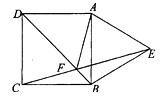
A.60°
B.50°
C.45°
D.40° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( ) .
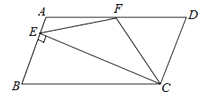
①∠DCF=∠BCD;②EF=CF;③S△BEC =2S△CEF;④∠DFE=3∠AEF.
A.①②③
B.①③
C.①②④
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应“足球进校园”的目标,光明中学准备购买一批足球,若购买2个A品牌足球和3个B品牌足球共需340元,购买5个A品牌足球和2个B品牌足球共需410元.
(1)购买一个A品牌足球、一个B品牌足球各需多少元?
(2)根据学校的实际情况,需购买两种品牌足球共50个,并且总费用不超过3120元.问最多可以购买多少个B品牌足球?
相关试题

