【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣1),B(﹣3,3),C(﹣4,1)
(1)画出△ABC关于y轴对称的△A1B1C1 , 并写出点B的对应点B1的坐标;
(2)画出△ABC绕点A按逆时针旋转90°后的△AB2C2 , 并写出点C的对应点C2的坐标.
参考答案:
【答案】
(1)
解:如图所示,△A1B1C1即为△ABC关于y轴对称的图形;
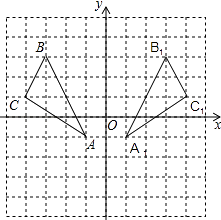
则B1的坐标是(3,3)
(2)
解:△ABC绕点A按逆时针旋转90°后的△AB2C2是:
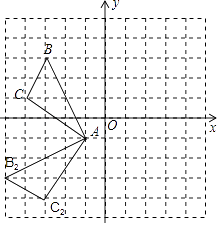
则点C的对应点C2的坐标是(﹣3,﹣4)
【解析】(1)补充成网格结构,然后找出点A、B、C关于y轴的对称点A1、B1、C1的位置,再顺次连接即可;再根据平面直角坐标系写出点B1的坐标;(2)根据旋转的性质画出△ABC绕点A按逆时针方向旋转90°后的△AB2C2 , 写出点C2的坐标即可.
【考点精析】根据题目的已知条件,利用作轴对称图形的相关知识可以得到问题的答案,需要掌握画对称轴图形的方法:①标出关键点②数方格,标出对称点③依次连线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:
①∠BOE=70°; ②OF平分∠BOD;③∠POE=∠BOF; ④∠POB=2∠DOF.
其中正确的结论有_______________(填结论前面的序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF

(1)求证:BF=DC;
(2)求证:四边形ABFD是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF//AD,
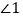 =
=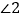 .说明:∠DGA+∠BAC=180°. 填空并写出推理的依据.
.说明:∠DGA+∠BAC=180°. 填空并写出推理的依据.
解:∵EF//AD,(已知)
∴
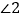 =__ __ (_____________________________)
=__ __ (_____________________________)
又∵
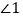 =
=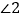 , (已知)
, (已知)∴
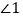 =__ _, (等量替代)
=__ _, (等量替代)∴AB//___ ___, (_______________ _____________)
∴∠DGA+∠BAC=180° (_______________ _________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,顶点A、B的坐标分别是A(1,0),B(0,﹣2),顶点C、D在双曲线y=
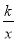 上,边AD与y轴相交于点E,S四边形BEDC=5S△ABE=10,则k的值是( )
上,边AD与y轴相交于点E,S四边形BEDC=5S△ABE=10,则k的值是( )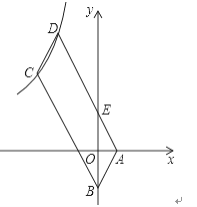
A. -16 B. -9 C. -8 D. -12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线OB是一次函数y=2x的图象,点A的坐标是(0,2),点C在直线OB上且△ACO为等腰三角形,求C点坐标.
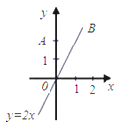
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)列式:x与20的差不小于0;
(2)若(1)中的x(单位:cm)是一个正方形的边长,现将正方形的边长增加2cm,则正方形的面积至少增加多少?
相关试题

