【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)若∠ABE=15°,∠BAD=40°,则∠BED=________°;
(2)请在图中作出△BED中BD边上的高EF;
(3)若△ABC的面积为40,BD=5,则点E到BC边的距离为多少?

参考答案:
【答案】(1)55 (2)见解析;(3)点E到BC边的距离为4.
【解析】
(1)利用外角性质解题,(2)见详解,(3)根据中线平分三角形面积这一性质解题.
∠BED=∠ABE+∠BAD=15°+40°=55°
故答案为:55
(2)见下图,

(3)∵AD为△ABC的中线,
∴S△ABD=![]() S△ABC=20.
S△ABC=20.
又∵BE为△ABD的中线,
∴S△BDE=![]() S△ABD=10.
S△ABD=10.
设点E到BC边的距离为h,
则![]() BD·h=10,
BD·h=10,
∴h=4.
即点E到BC边的距离为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,BP是△ABC中∠ABC的平分线,CP是△ABC的外角∠ACM的平分线,如果∠ABP=20°,∠ACP=50°,那么∠A+∠P的度数为( )

A. 60° B. 70° C. 80° D. 90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象的顶点C的坐标为(0,﹣2),交x轴于A、B两点,其中A(﹣1,0),直线l:x=m(m>1)与x轴交于D.
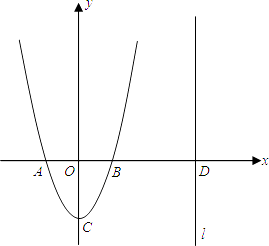
(1)求二次函数的解析式和B的坐标;
(2)在直线l上找点P(P在第一象限),使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似,求点P的坐标(用含m的代数式表示);
(3)在(2)成立的条件下,在抛物线上是否存在第一象限内的点Q,使△BPQ是以P为直角顶点的等腰直角三角形?如果存在,请求出点Q的坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心.重心有很多美妙的性质,如关于线段比.面积比就有一些“漂亮”结论,利用这些性质可以解决三角形中的若干问题.请你利用重心的概念完成如下问题:
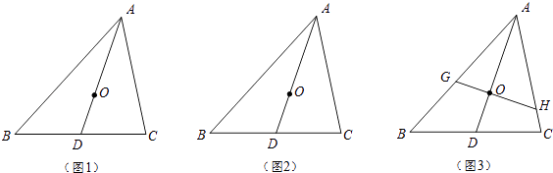
(1)若O是△ABC的重心(如图1),连结AO并延长交BC于D,证明: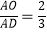 ;
;
(2)若AD是△ABC的一条中线(如图2),O是AD上一点,且满足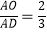 ,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
(3)若O是△ABC的重心,过O的一条直线分别与AB、AC相交于G、H(均不与△ABC的顶点重合)(如图3),S四边形BCHG , S△AGH分别表示四边形BCHG和△AGH的面积,试探究 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. ×(﹣3)=1
×(﹣3)=1
B.5﹣8=﹣3
C.2﹣3=6
D.(﹣2013)0=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB>AC,∠AEF=∠AFE,EF与BC的延长线交于点G,试说明:∠G=
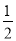 (∠ACB-∠B).
(∠ACB-∠B).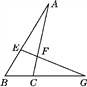
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(3,5)在直线y=ax+b(a,b为常数,且a≠0)上,则
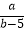 的值为 .
的值为 .
相关试题

