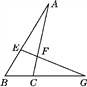
【题目】如图,在△ABC中,AB>AC,∠AEF=∠AFE,EF与BC的延长线交于点G,试说明:∠G=![]() (∠ACB-∠B).
(∠ACB-∠B).
参考答案:
【答案】见解析
【解析】【试题分析】
因为∠AEF=∠AFE,∠AFE=∠GFC,根据等量代换,∠AEF=∠GFC;根据三角形的外角性质得:∠AEF=∠B+∠G,所以∠GFC=∠B+∠G;根据三角形的外角性质得:∠ACB=∠GFC+∠G,代入即可,∠ACB=∠B+2∠G;根据等式的性质得:∠G=![]() (∠ACB-∠B).
(∠ACB-∠B).
【试题解析】
因为∠AEF=∠AFE,∠AFE=∠GFC,
所以∠AEF=∠GFC.
因为∠AEF=∠B+∠G,
所以∠GFC=∠B+∠G.
又因为∠ACB=∠GFC+∠G,
所以∠ACB=∠B+2∠G.
所以∠G=![]() (∠ACB-∠B).
(∠ACB-∠B).
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心.重心有很多美妙的性质,如关于线段比.面积比就有一些“漂亮”结论,利用这些性质可以解决三角形中的若干问题.请你利用重心的概念完成如下问题:
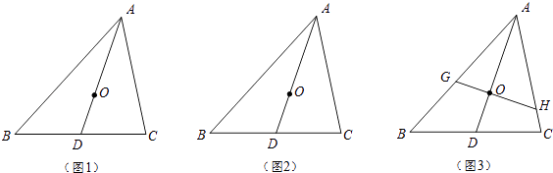
(1)若O是△ABC的重心(如图1),连结AO并延长交BC于D,证明: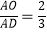 ;
;
(2)若AD是△ABC的一条中线(如图2),O是AD上一点,且满足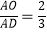 ,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
(3)若O是△ABC的重心,过O的一条直线分别与AB、AC相交于G、H(均不与△ABC的顶点重合)(如图3),S四边形BCHG , S△AGH分别表示四边形BCHG和△AGH的面积,试探究 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)若∠ABE=15°,∠BAD=40°,则∠BED=________°;
(2)请在图中作出△BED中BD边上的高EF;
(3)若△ABC的面积为40,BD=5,则点E到BC边的距离为多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. ×(﹣3)=1
×(﹣3)=1
B.5﹣8=﹣3
C.2﹣3=6
D.(﹣2013)0=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(3,5)在直线y=ax+b(a,b为常数,且a≠0)上,则
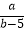 的值为 .
的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.符合题意的组建方案有( )种.
A. 1种 B. 2种 C. 3种 D. 4种
-
科目: 来源: 题型:
查看答案和解析>>【题目】2013成都)若正整数n使得在计算n+(n+1)+(n+2)的过程中,各数位均不产生进位现象,则称n为“本位数”.例如2和30是“本位数”,而5和91不是“本位数”.现从所有大于0且小于100的“本位数”中,随机抽取一个数,抽到偶数的概率为 .
相关试题

