【题目】互联网时代,发达的物流业改变了我们的生活.某快递公司的分发中心、菜鸟驿站、快递员公寓依次分布在同一条直线上,快递员甲、乙分别同时从菜鸟驿站和分发中心出发,甲先骑自行车回到分发中心,将自行车归还分发中心后步行经过菜鸟驿站返回公寓(归还自行车的时间忽略不计),乙先从分发中心步行到菜鸟驿站,步行速度与甲的步行速度相同,到达菜鸟驿站后停下来继续完成剩余工作,随后跑步回公寓,最后两人同时到达公寓.甲、乙两人与公寓的距离y(米)与出发的时间x(分钟)之间的关系如图所示.
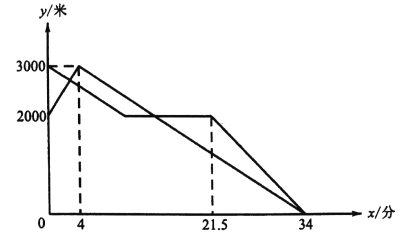
(1)甲骑自行车的速度为 米/分,乙跑步的速度为 米/分;
(2)乙在菜鸟驿站停留的时间为 分钟;
(3)甲乙第二次相遇后再经过多少分钟他们相距450米?
参考答案:
【答案】(1)250,160;(2)11.5;(3)甲乙第二次相遇后再经过4.5分钟或19![]() 分钟他们相距450米.
分钟他们相距450米.
【解析】
(1)根据分发中心与菜鸟驿站间的距离,根据速度=路程÷时间可求出甲骑自行车的速度,由菜鸟驿站与公寓的距离,根据速度=路程÷时间可求出乙跑步的速度;
(2)先求出甲步行的速度,然后求出乙从分发中心到菜鸟驿站所用时间,继而可求得答案;
(3)先分别求出甲从分发中心返回公寓过程中与公寓的距离y(米)与出发的时间x(分钟)之间的关系式,乙跑步过程中与公寓的距离y(米)与出发的时间x(分钟)之间的关系式,然后再分乙在分发中心、乙跑步两种情况分别讨论即可得.
(1)甲骑自行车的速度为:(3000-2000)÷4=250米/分,
由图象可知菜鸟驿站离公寓2000米,
所以乙跑步的速度为2000÷(34-21.5)=160米/分,
故答案为:250,160;
(2)甲步行的速度为:3000÷(34-4)=100米/分,
所以乙从分发中心到菜鸟驿站所用时间为(3000-2000)÷100=10分钟,
21.5-10=11.5分钟,
故答案为:11.5;
(3)设甲从分发中心返回公寓过程中与公寓的距离y(米)与出发的时间x(分钟)之间的关系式为y甲=k1x+b1,
由题意则有 ,解得
,解得 ,
,
所以解析式为:y=-100x+3400,
设乙跑步过程中与公寓的距离y(米)与出发的时间x(分钟)之间的关系式为y乙=k2x+b2,
由题意则有 ,解得
,解得 ,
,
所以解析式为:y乙=-160x+5440,
当乙在分发中心时,
当y甲=2000时,-100x+3400=2000,x=14,即出发14分钟时甲乙第二次相遇,
当y甲=2000-450=1550时,-100x+3400=1550,x=18.5,18.5-14=4.5分钟,
即甲乙第二次相遇后再经过4.5分钟他们相距450米;
当乙跑步时,-160x+5440-(-100x+3400)=450,x=33![]() ,
,
33![]() -14=19
-14=19![]() (分钟),
(分钟),
即甲乙第二次相遇后再经过19![]() 分钟他们相距450米,
分钟他们相距450米,
综上,甲乙第二次相遇后再经过4.5分钟或19![]() 分钟他们相距450米.
分钟他们相距450米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两班举行电脑汉字输入比赛,各选10名选手参赛,各班参赛学生每分钟输入汉字个数统计如下表:
输入汉字个数(个)
132
133
134
135
136
137
甲班人数人)
1
0
2
4
1
2
乙班人数(人)
0
1
4
1
2
2
请分别判断下列同学是说法是否正确,并说明理由.
(1)两个班级输入汉字个数的平均数相同;
(2)两个班学生输入汉字的中位数相同众数也相同;
(3)甲班学生比乙班学生的成绩稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只不透明的袋子中装有4个大小、质地都相同的乒乓球,球面上分别标有数字1、2、3、4.
(1)搅匀后从中任意摸出1个球,求摸出的乒乓球球面上数字为1的概率;
(2)搅匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,求2次摸出的乒乓球球面上数字之和为偶数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了调查本校初2021级学生的跳绳水平,抽取了某班60名学生的跳绳成绩(满分为10分,分数均为自然数),绘制如下两幅不完整的统计图.请根据统计图的信息,回答下列问题.

(1)在扇形统计图中,
 的值是 ,成绩为10分所在扇形的圆心角是 度;
的值是 ,成绩为10分所在扇形的圆心角是 度;(2)补全条形统计图;
(3)若从该班男生中随机抽取一人,求这名男生跳绳成绩不是10分的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在
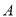 处测得灯塔
处测得灯塔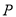 在北偏东
在北偏东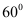 方向上,继续航行1小时到达
方向上,继续航行1小时到达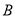 处,此时测得灯塔
处,此时测得灯塔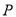 在北偏东
在北偏东 方向上.
方向上.(1)求
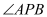 的度数;
的度数;(2)已知在灯塔
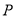 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 的一元二次方程
的一元二次方程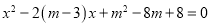
⑴说明该方程根的情况.
⑵若
 (
( 为整数),且方程有两个整数根,求
为整数),且方程有两个整数根,求 的值.
的值. -
科目: 来源: 题型:
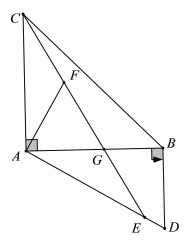
查看答案和解析>>【题目】如图,在△ABC和△ABD中,∠BAC=∠ABD=90°,点E为AD边上的一点,且AC=AE,连接CE交AB于点G,过点A作AF⊥AD交CE于点F.
(1)求证:△AGE≌△AFC;
(2)若AB=AC,求证:AD=AF+BD.
相关试题

