搜索
【题目】一只不透明的袋子中装有4个大小、质地都相同的乒乓球，球面上分别标有数字1、2、3、4．
（1）搅匀后从中任意摸出1个球，求摸出的乒乓球球面上数字为1的概率；
（2）搅匀后先从中任意摸出1个球（不放回），再从余下的3个球中任意摸出1个球，求2次摸出的乒乓球球面上数字之和为偶数的概率．
参考答案：
【答案】(1) 
；（2）
.
【解析】试题分析：（1）根据袋子中球的个数和球面上分别标有的数字，再根据概率公式即可得出答案；
（2）根据题意先画出树状图，得出所以等可能的结果数和2次摸出的乒乓球球面上数字之和为偶数的结果数，然后根据概率公式求解即可．
试题解析：解：（1）∵共有4个大小、质地都相同的乒乓球，球面上分别标有数字1、2、3、4，∴摸出的乒乓球球面上数字为1的概率是
；
（2）根据题意画树状图如下：
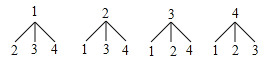
共有12种等可能的结果，两次摸出的乒乓球球面上的数字的和为偶数的有4种情况，则两次摸出的乒乓球球面上的数字的和为偶数的概率为
=
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】探索:
(x-1)(x+1)=x2-1, (x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1, (x-1)(x4+x3+x2+x+1)=x5-1,
……
(1)试写出第五个等式;
(2)试求26+25+24+23+22+2+1的值;
(3)判断22 017+22 016+22 015+…+22+2+1的值的个位数字是几.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线CD与EF相交于点O，∠COE=60°，将一直角三角尺AOB的直角顶点与O重合，OA平分∠COE．
（1）求∠BOD的度数；
（2）将三角尺AOB以每秒3°的速度绕点O顺时针旋转，同时直线EF也以每秒9°的速度绕点O顺时针旋转，设运动时间为t秒（0≤t≤40）．
①当t为何值时，直线EF平分∠AOB；
②若直线EF平分∠BOD，直接写出t的值．
-
科目： 来源： 题型：
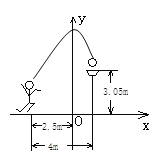
查看答案和解析>>【题目】如图所示,一位篮球运动员在离篮圈水平距离为4m处跳起投篮,球沿一条抛物线运行,当球运行的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心离地面距离为3.05m.
(1)建立如图所示的直角坐标系,求抛物线所对应的函数关系式;
(2)若该运动员身高1.8m,这次跳投时,球在他头顶上方0.25m处出手.问:球出手时,他跳离地面多高?
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的边AB在数轴上，数轴上点A表示的数为﹣1，正方形ABCD的面积为16．
（1）数轴上点B表示的数为 ；
（2）将正方形ABCD沿数轴水平移动，移动后的正方形记为A′B′C′D′，移动后的正方形A′B′C′D′与原正方形ABCD重叠部分的面积为S．
①当S=4时，画出图形，并求出数轴上点A′表示的数；
②设正方形ABCD的移动速度为每秒2个单位长度，点E为线段AA′的中点，点F在线段BB′上，且BF=
BB′．经过t秒后，点E，F所表示的数互为相反数，直接写出t的值． -
科目： 来源： 题型：
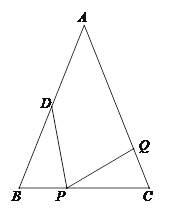
查看答案和解析>>【题目】如图，已知△ABC中，AB=AC=6cm，BC=4cm，点D为AB的中点．
⑴如果点P在线段BC上以1cm/s的速度由点B向点C运动，同时，点Q在线段CA上由点C向点A运动．
①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CPQ是否全等，请说明理由；
②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为______cm/s时，在某一时刻也能够使△BPD与△CPQ全等．
⑵若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都按逆时针方向沿△ABC的三边运动．求经过多少秒后，点P与点Q第一次相遇，并写出第一次相遇点在△ABC的哪条边上？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示， AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3=_____.
相关试题
