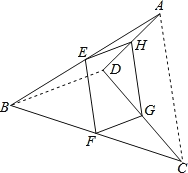
【题目】如图,E、F、G、H分别为四边形ABCD四边之中点.
(1)求证:四边形EFGH为平行四边形;
(2)当AC、BD满足 时,四边形EFGH为菱形.当AC、BD满足 时,四边形EFGH为矩形.当AC、BD满足 时,四边形EFGH为正方形.

参考答案:
【答案】(1)证明见解析;(2)AC=BD;AC⊥BD;AC=BD且AC⊥BD.
【解析】
(1)连接BD,根据三角形的中位线平行于第三边并且等于第三边的一半可得EH∥BD且EH=![]() BD,FG∥BD且FG=
BD,FG∥BD且FG=![]() BD,从而得到EH∥FG且EH=FG,再根据一组对边平行且相等的四边形是平行四边形证明即可;
BD,从而得到EH∥FG且EH=FG,再根据一组对边平行且相等的四边形是平行四边形证明即可;
(2)连接AC,同理可得EF∥AC且EF=![]() AC,再根据邻边相等的平行四边形是菱形,邻边垂直的平行四边形是矩形,邻边相等且垂直的平行四边形是正方形解答.
AC,再根据邻边相等的平行四边形是菱形,邻边垂直的平行四边形是矩形,邻边相等且垂直的平行四边形是正方形解答.
(1)如图,连接BD.
∵E、F、G、H分别为四边形ABCD四边之中点,
∴EH是△ABD的中位线,FG是△BCD的中位线,
∴EH∥BD且EH=![]() BD,FG∥BD且FG=
BD,FG∥BD且FG=![]() BD,
BD,
∴EH∥FG且EH=FG,
∴四边形EFGH为平行四边形;
(2)连接AC,
同理可得EF∥AC且EF=![]() AC,
AC,
所以,AC=BD时,四边形EFGH为菱形;
AC⊥BD时,四边形EFGH为矩形;
AC=BD且AC⊥BD时,四边形EFGH为正方形.
故答案为:AC=BD;AC⊥BD;AC=BD且AC⊥BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班在布置新年联欢会场,需要将直角三角形彩纸裁成长度不等的矩形彩条,如图所示,在Rt△ABC中,∠C=90°,AC=30cm,AB=50cm,依次裁下宽为1cm 的矩形纸条a1,a2,a3,…,若使裁得的矩形纸条的长都不小于5cm,问,每张直角三角形彩纸能裁成的矩形纸条总数是多少?

-
科目: 来源: 题型:
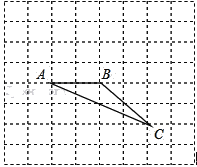
查看答案和解析>>【题目】如图在8×8的正方形网格中,△ABC 的顶点在边长为1的小正方形的顶点上.
(1)填空:∠ABC= ,BC= ;
(2)若点A在网格所在的坐标平面里的坐标为(1,﹣2),请你在图中找出一点D,并作出以A、B、C、D四个点为顶点的平行四边形,求出满足条件的D点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下表中的二次函数y=ax2+bx+c的自变量x与函数y的对应值,可判断二次函数的解析式为( )
x
…

0
1
2
…
y
…



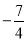
…
A. y=
 x2﹣
x2﹣ x﹣
x﹣ B. y=
B. y= x2+
x2+ x﹣
x﹣
C. y=﹣
 x2﹣
x2﹣ x+
x+ D. y=﹣
D. y=﹣ x2+
x2+ x+
x+
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三角形△ABC中,D是BC边的中点,AD=
 BC.
BC.(1)△ABC的形状为 .
(2)如图,BM=3,BC=12,∠B=45°,∠MAN=45°,求CN;
(3)在(2)的条件下,AN= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数的图象经过原点及点(
 ,
, ),且图象与x轴的另一交点到原点的距离为1,则该二次函数解析式为 .
),且图象与x轴的另一交点到原点的距离为1,则该二次函数解析式为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解七年级学生的身体素质情况,体育老师对该年级部分学生进行了一分钟跳绳次数的测试,并把测试成绩绘制成如图所示的频数表和频数直方图(每组含前一个边界值,不含后一个边界值).


(1)参加测试的学生有多少人?
(2)求
 ,
, 的值,并把频数直方图补充完整.
的值,并把频数直方图补充完整.(3)若该年级共有
 名学生,估计该年级学生一分钟跳绳次数不少于
名学生,估计该年级学生一分钟跳绳次数不少于 次的人数.
次的人数.
相关试题

