搜索
【题目】已知二次函数的图象经过原点及点（
，
），且图象与x轴的另一交点到原点的距离为1，则该二次函数解析式为 ．
参考答案：
【答案】y=-
x2+x；y=x2+x．
【解析】
试题分析：设二次函数的解析式为y=ax2+bx+c（a≠0），由图象与x轴的另一交点到原点的距离为1可得到抛物线与x轴的另一交点坐标为（1，0）或（-1，0），然后分别把（0，0）、（1，0）、（-
，-
）或（0，0）、（-1，0）、（-，-）代入解析式中得到两个方程组，解方程组即可确定解析式．
试题解析：设二次函数的解析式为y=ax2+bx+c（a≠0），
当图象与x轴的另一交点坐标为（1，0）时，
把（0，0）、（1，0）、（-，-）代入得
，
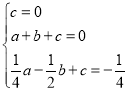解方程组得
，
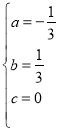则二次函数的解析式为y=-x2+x；
当图象与x轴的另一交点坐标为（-1，0）时，得
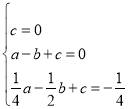
解方程组得
，
则二次函数的解析式为y=x2+x．
所以该二次函数解析式为: y=-x2+x；y=x2+x．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面解答过程，并填空或填理由．
已知如下图，点E、F分别是AB和CD上的点，DE、AF分别交BC于点G、H，∠A=∠D，∠1=∠2．
试说明：∠B=∠C．
解：∵∠1=∠2（已知）
∠2=∠3（___________）
∴∠3=∠1（等量代换）
∴AF∥DE（___________）
∴∠4=∠D（___________）
又∵∠A=∠D（已知）
∴∠A=∠4（等量代换）
∴AB∥CD（___________）
∴∠B=∠C（___________）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直角三角形ABC中，∠C=90°，点O为AB上的一点，以点O为圆心，OA为半径的圆弧与BC相切于点D，交AC于点E，连接AD．
（1）求证：AD平分∠BAC；
（2）已知AE=2，DC=
，求圆弧的半径．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点P为∠AOB的角平分线上的一点，点D在边OA上．爱动脑筋的小刚经过仔细观察后，进行如下操作：在边OB上取一点E，使得PE=PD，这时他发现∠OEP与∠ODP之间有一定的数量关系，请你写出∠OEP与∠ODP所有可能的数量关系是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某单位准备印制一批证书，现有两个印刷厂可供选择，甲厂费用分为制版费和印刷费两部分，乙厂直接按印刷数量收取印刷费．甲乙两厂的印刷费用y（千元）与证书数量x（千个）的函数关系图象分别如图中甲、乙所示．
（1）填空：甲厂的制版费是________千元，当x≤2（千个）时乙厂证书印刷单价是________元/个；
（2）求出甲厂的印刷费y甲与证书数量x的函数关系式，并求出其证书印刷单价；
（3）当印制证书8千个时，应选择哪个印刷厂节省费用，节省费用多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知x=﹣3是关于x的方程（k+3）x+2=3x﹣2k的解．
（1）求k的值；
（2）在（1）的条件下，已知线段AB=6cm，点C是直线AB上一点，且BC=kAC，若点D是AC的中点，求线段CD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】求出符合条件的二次函数解析式：
（1）二次函数图象经过点（﹣1，0），（1，2），（0，3）；
（2）二次函数图象的顶点坐标为（﹣3，6），且经过点（﹣2，10）；
（3）二次函数图象与x轴的交点坐标为（﹣1，0），（3，0），与y轴交点的纵坐标为9．
相关试题
