【题目】在三角形△ABC中,D是BC边的中点,AD=![]() BC.
BC.
(1)△ABC的形状为 .
(2)如图,BM=3,BC=12,∠B=45°,∠MAN=45°,求CN;
(3)在(2)的条件下,AN= .

参考答案:
【答案】(1)直角三角形;(2)CN=4;(3)![]() .
.
【解析】
(1)已知BD=DC,AD=![]() BC,得DA=DB=DC,所以
BC,得DA=DB=DC,所以![]() ,又因为
,又因为![]() ,可得∠BAC=
,可得∠BAC=![]() ,所以△ABC为直角三角形.
,所以△ABC为直角三角形.
(2)设CN=x.ACB=∠B=45°,可得AB=AC.因为BD=DC,可得AD⊥BC,将△BAM绕点A逆时针旋转90°得到△ACH,连接NH.证明△NAM≌△NAH,可得MN=NH.根据NH2=CH2+CN2,列出方程(9﹣x)2=x2+32,解得CN=x=4
(3)在Rt△ADN中,∠ADN=90°,AD= 6,DN=2,利用勾股定理即可求得AN=![]()
(1)结论:△ABC是直角三角形.
理由:∵BD=DC,AD=![]() BC,
BC,
∴DA=DB=DC,
∴![]()
∵![]()
∴∠BAC=![]()
故答案为:直角三角形.
(2)如图,设CN=x.

∵∠B=45°,∠BAC=90°,
∴∠ACB=∠B=45°,
∴AB=AC.
∵BD=DC,
∴AD⊥BC,
将△BAM绕点A逆时针旋转90°得到△ACH,连接NH.
∵∠ACB=∠ACH=∠B=45°,
∴∠NCH=90°.
∵∠MAN=45°,∠MAH=90°,
∴∠NAM=∠NAH=45°.
∵NA=NA,AM=AH,
∴△NAM≌△NAH(SAS),
∴MN=NH.
∵BM=CH=3,BC=12,
∴CM=12﹣3=9,
∴MN=NH=9﹣x.
∵NH2=CH2+CN2,
∴(9﹣x)2=x2+32,
解得:x=4,
∴CN=4.
(3)在Rt△ADN中,
∵∠ADN=90°,AD=BD=CD=6,DN=CD﹣CN=6﹣4=2,
∴AN=![]()
故答案为:![]()
-
科目: 来源: 题型:
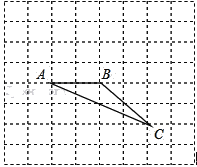
查看答案和解析>>【题目】如图在8×8的正方形网格中,△ABC 的顶点在边长为1的小正方形的顶点上.
(1)填空:∠ABC= ,BC= ;
(2)若点A在网格所在的坐标平面里的坐标为(1,﹣2),请你在图中找出一点D,并作出以A、B、C、D四个点为顶点的平行四边形,求出满足条件的D点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下表中的二次函数y=ax2+bx+c的自变量x与函数y的对应值,可判断二次函数的解析式为( )
x
…

0
1
2
…
y
…



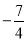
…
A. y=
 x2﹣
x2﹣ x﹣
x﹣ B. y=
B. y= x2+
x2+ x﹣
x﹣
C. y=﹣
 x2﹣
x2﹣ x+
x+ D. y=﹣
D. y=﹣ x2+
x2+ x+
x+
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E、F、G、H分别为四边形ABCD四边之中点.
(1)求证:四边形EFGH为平行四边形;
(2)当AC、BD满足 时,四边形EFGH为菱形.当AC、BD满足 时,四边形EFGH为矩形.当AC、BD满足 时,四边形EFGH为正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数的图象经过原点及点(
 ,
, ),且图象与x轴的另一交点到原点的距离为1,则该二次函数解析式为 .
),且图象与x轴的另一交点到原点的距离为1,则该二次函数解析式为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解七年级学生的身体素质情况,体育老师对该年级部分学生进行了一分钟跳绳次数的测试,并把测试成绩绘制成如图所示的频数表和频数直方图(每组含前一个边界值,不含后一个边界值).


(1)参加测试的学生有多少人?
(2)求
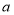 ,
, 的值,并把频数直方图补充完整.
的值,并把频数直方图补充完整.(3)若该年级共有
 名学生,估计该年级学生一分钟跳绳次数不少于
名学生,估计该年级学生一分钟跳绳次数不少于 次的人数.
次的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中A(a,0),B(b,0),D(0,d),以AB,AD为邻边做平行四边形ABCD,其中a,b,d满足
 .
.(1)求出C的坐标,及平行四边形ABCD的面积;
(2)如图2,线段BC的中垂线交y轴与点E,F为AD的中点,试判断∠EFB的大小,并说明理由;
(3)如图3,过点C作CG⊥x轴与点G,K为线段DG上的一点,KH⊥CK交OG延长线与点H,且∠DKC=3∠KHG,请求出
 的值.
的值.
相关试题

