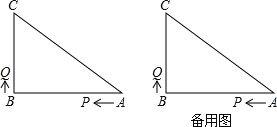
【题目】如图,在△ABC中,∠B=90°,AB=8厘米,BC=6厘米,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动速度为1厘米/秒,点Q从点B开始沿B→C→A方向运动速度为2厘米/秒,若它们同时出发,设出发的时间为t秒.
(1)求出发2秒后,PQ的长;
(2)点Q在CA边上运动时,当△BCQ成为等腰三角形时,求点Q的运动时间.
参考答案:
【答案】(1)![]() 厘米;(2)当t为5.5秒或6秒或6.6秒时,△BCQ为等腰三角形.
厘米;(2)当t为5.5秒或6秒或6.6秒时,△BCQ为等腰三角形.
【解析】
(1)运动2秒后,根据P、Q运动速度可知道运动的路程BQ和AP长,在Rt△QBP中,利用勾股定理即可求出PQ.
(2)已知点Q在CA边上运动时,若△BCQ成为等腰三角形,可分三种情况讨论,即CQ=BQ,CQ=BC,BC=BQ,得出点Q运动的路程,已知速度即可求出运动时间,在直角三角形中可利用勾股定理求解.
(1)BQ=2×2=4cm,
BP=AB﹣AP=8﹣2×1=6cm.
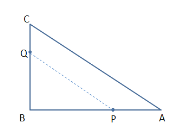
∵∠B=90°,
PQ=![]() (cm);
(cm);
故答案为:![]() 厘米
厘米
(2)分三种情况:
①当CQ=BQ时,如图1所示:
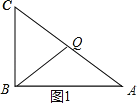
则∠C=∠CBQ.
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°,
∵∠A+∠C=90°,
∴∠A=∠ABQ
∴BQ=AQ,
∴BQ是Rt△ABC斜边上的中线
∵AC=![]()
∴CQ=AQ=5,
∴BC+CQ=11,
∴t=11÷2=5.5秒.
②当CQ=BC时,如图2所示:
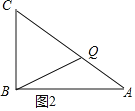
则BC+CQ=12
∴t=12÷2=6秒.
③当BC=BQ时,如图3所示:
过B点作BE⊥AC于点E,
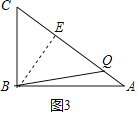
则BE![]() (cm)
(cm)
∴CE=![]() cm,
cm,
∴CQ=2CE=7.2cm,
∴BC+CQ=13.2cm,
∴t=13.2÷2=6.6秒.
综上所述,当t为5.5秒或6秒或6.6秒时,
△BCQ为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与X轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:
①4a﹣2b+c<0;②2a﹣b<0;③a+c<1;④b2+8a>4ac,
其中正确的有( )

A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,点
中,点 的坐标为(0,4),线段
的坐标为(0,4),线段 的位置如图所示,其中点
的位置如图所示,其中点 的坐标为(
的坐标为( ,
, ),点
),点 的坐标为(3,
的坐标为(3, ).
).
(1)将线段
 平移得到线段
平移得到线段 ,其中点
,其中点 的对应点为
的对应点为 ,点
,点 的对应点为点
的对应点为点 .
.①点
 平移到点
平移到点 的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;②点
 的坐标为 .
的坐标为 .(2)在(1)的条件下,若点
 的坐标为(4,0),连接
的坐标为(4,0),连接 ,画出图形并求
,画出图形并求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为
 ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.分数段
频数
百分比

38
0.38

0.32

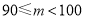
10
0.1
合计
100
1
书法作品比赛成绩频数直方图

根据上述信息,解答下列问题:
(1)请你把表中空白处的数据填写完整.
(2)请补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级的幅数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将抛物线C1:y=x2绕点(1,0)旋转180°后,得到抛物线C2,定义抛物线C1和C2上位于﹣2≤x≤2范围内的部分为图象C3.若一次函数y=kx+k﹣1(k>0)的图象与图象C3有两个交点,则k的范围是:__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,青少年中的近视眼和肥胖案例日趋增多,人们普遍意识到健康的身体是学习的保障,所以体育活动越来越受重视.某商店分两次购进跳绳和足球两种商品进行销售,每次购进同一种商品的进价相同,具体情况如下表所示.
购进数量(件)
购进所需费用(元)
跳绳
足球
第一次
30
40
3800
第二次
40
30
3200
(1)跳绳和足球两种商品每件的进价分别是多少元?
(2)商店计划用5300元的资金进行第三次进货,共购进跳绳和足球两种商品100件,其中要求足球的数量不少于跳绳的数量,有哪几种进货方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在4×4的正方形(每个小正方形的边长均为1)网格中,以A为顶点,其他三个顶点都在格点(网格的交点)上,且面积为2的平行四边形共有多少个?( )

A.12B.16C.24D.25
相关试题

