【题目】近年来,青少年中的近视眼和肥胖案例日趋增多,人们普遍意识到健康的身体是学习的保障,所以体育活动越来越受重视.某商店分两次购进跳绳和足球两种商品进行销售,每次购进同一种商品的进价相同,具体情况如下表所示.
购进数量(件) | 购进所需费用(元) | ||
跳绳 | 足球 | ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1)跳绳和足球两种商品每件的进价分别是多少元?
(2)商店计划用5300元的资金进行第三次进货,共购进跳绳和足球两种商品100件,其中要求足球的数量不少于跳绳的数量,有哪几种进货方案?
参考答案:
【答案】(1)每根跳绳的进价为20元,每个足球的进价为80元;(2)共有以下6种进货方案,具体方案见解析.
【解析】
(1)设跳绳的进价为x元,足球的进价为y元,根据前两次进货的数量及总价,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购进跳绳m根,则购进足球(100-m)个,由B商品的数量不少于A商品的数量且总价不超过5300元,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,结合m为整数即可得出各进货方案.
(1)设每根跳绳的进价为![]() 元,每个足球的进价为
元,每个足球的进价为![]() 元.
元.
依题意,得![]() 解得
解得![]()
答:每根跳绳的进价为20元,每个足球的进价为80元.
(2)设购进跳绳![]() 根,则购进足球
根,则购进足球![]() 个.
个.
由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,则有
,则有![]() .
.
∵![]() 为整数,∴
为整数,∴![]() 的值可能为45,46,47,48,49,50,
的值可能为45,46,47,48,49,50,
∴共有以下6种进货方案:
方案一:购进跳绳45根,则购进足球55个.
方案二:购进跳绳46根,则购进足球54个.
方案三:购进跳绳47根,则购进足球53个.
方案四:购进跳绳48根,则购进足球52个.
方案五:购进跳绳49根,则购进足球51个.
方案六:购进跳绳50根,则购进足球50个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.
(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°;
①求∠OCE的度数. ②若⊙O的半径为
 ,求线段CF的长.
,求线段CF的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一张三角形纸片ABC(如图甲),其中AB=AC.将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为EF(如图丙).原三角形纸片ABC中,∠ABC的大小为______°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为1的等边三角形,过点C的直线m平行AB,D、E分别是线段AB、直线m上的点,先按如图方式进行折叠,点A、C分别落在A′、C′处,且A′C′经过点B,DE为折痕,当C′E⊥m时,
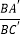 的值为_____.
的值为_____.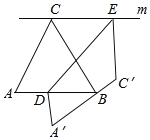
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣
 x2+
x2+ x+4经过A、B两点.
x+4经过A、B两点.
(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,是否存在t,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若
 ,是
,是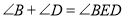 .
.
理由:如图,过点
 作
作 ,
,则
 .(依据)
.(依据)因为
 ,
,所以
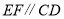 ,
,所以
 .
.所以
 .
.(1)上述证明过程中的依据是指 .
(2)若将点
 移至图2所示的位置,
移至图2所示的位置, ,此时
,此时 之间有什么关系?请说明理由.
之间有什么关系?请说明理由.
(3)在图中,
 ,
, 与
与 又有何关系?
又有何关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:


(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
相关试题

